Інтегральне правило Лейбніца

Нехай f(x, t) — це функція така, що часткова похідна f щодо t існує і є неперервною. Тоді,

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}\left(\int _{a(t)}^{b(t)}f(x,t)\,\mathrm {d} x\right)=\int _{a(t)}^{b(t)}{\frac {\partial f}{\partial t}}\,\mathrm {d} x\,+\,f{\big (}b(t),t{\big )}\cdot b'(t)\,-\,f{\big (}a(t),t{\big )}\cdot a'(t)}$

Нехай

${\displaystyle \varphi (\alpha )=\int _{a}^{b}f(x,\alpha )\,\mathrm {d} x,}$

де a і b — функції від α, що мають прирости Δa і Δb, відповідно, коли α збільшують на Δα. Тоді,

${\displaystyle {\begin{aligned}\Delta \varphi &=\varphi (\alpha +\Delta \alpha )-\varphi (\alpha )\\&=\int _{a+\Delta a}^{b+\Delta b}f(x,\alpha +\Delta \alpha )\,\mathrm {d} x-\int _{a}^{b}f(x,\alpha )\,\mathrm {d} x\\&=\int _{a+\Delta a}^{a}f(x,\alpha +\Delta \alpha )\,\mathrm {d} x+\int _{a}^{b}f(x,\alpha +\Delta \alpha )\,\mathrm {d} x+\int _{b}^{b+\Delta b}f(x,\alpha +\Delta \alpha )\,\mathrm {d} x-\int _{a}^{b}f(x,\alpha )\,\mathrm {d} x\\&=-\int _{a}^{a+\Delta a}f(x,\alpha +\Delta \alpha )\,\mathrm {d} x+\int _{a}^{b}[f(x,\alpha +\Delta \alpha )-f(x,\alpha )]\,\mathrm {d} x+\int _{b}^{b+\Delta b}f(x,\alpha +\Delta \alpha )\,\mathrm {d} x\end{aligned}}}$

Використовуючи теорему про середнє значення у формі, ${\displaystyle \int _{a}^{b}f(x)\,\mathrm {d} x=(b-a)f(\xi )}$, де a < ξ < b, до першого і останнього інтегралів у формулі для Δφ вище, маємо

${\displaystyle \Delta \varphi =-\Delta af(\xi _{1},\alpha +\Delta \alpha )+\int _{a}^{b}[f(x,\alpha +\Delta \alpha )-f(x,\alpha )]\,\mathrm {d} x+\Delta bf(\xi _{2},\alpha +\Delta \alpha )}$

Ділячи на Δα і спрямовуючи Δα → 0, і зауважуючи, що ξ₁ → a і ξ₂ → b, і використовуючи наступне

${\displaystyle \lim _{\Delta \alpha \to 0}\int _{a}^{b}{\frac {f(x,\alpha +\Delta \alpha )-f(x,\alpha )}{\Delta \alpha }}\,\mathrm {d} x=\int _{a}^{b}{\frac {\mathrm {d} }{\mathrm {d} \alpha }}f(x,\alpha )\,\mathrm {d} x}$

отримуємо загальну форму інтегрального правила Лейбніца:

${\displaystyle {\frac {\mathrm {d} \varphi }{\mathrm {d} \alpha }}=\int _{a}^{b}{\frac {\mathrm {d} }{\mathrm {d} \alpha }}f(x,\alpha )\,\mathrm {d} x+f(b,\alpha ){\frac {\mathrm {d} b}{\mathrm {d} \alpha }}-f(a,\alpha ){\frac {\mathrm {d} a}{\mathrm {d} \alpha }}}$

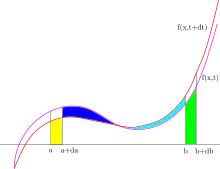
На зображенні горизонтальна вісь це вісь ${\displaystyle x}$. Ми маємо, що різні значення ${\displaystyle t}$ дають різні функції від ${\displaystyle x}$.

Згідно з правилом Лейбніца, границі ${\displaystyle a,b}$ змінюватимуться зі зміною ${\displaystyle t}$. Отже, зі зміною ${\displaystyle t}$ маємо три внески у зміну інтеграла:

1. Змінюється нижня границя. Площа під кривою зменшується приблизно на жовту область

   ${\displaystyle dA_{1}=-da\ f(x,a)=-dt{\frac {da}{dt}}f(x,a).}$

2. Змінюється верхня границя. Подібним чином

   ${\displaystyle dA_{2}=db\ f(x,b)=dt{\frac {db}{dt}}f(x,b).}$

3. Змінюється інтегранд. Його площа зменшується на синю область і збільшується на область морського кольору.

   ${\displaystyle dA_{3}=\int _{a}^{b}[f(x,t+dt)-f(x,t)]dx=\int _{a}^{b}{\frac {\delta f}{\delta t}}dt\ dx=dt\int _{a}^{b}{\frac {\delta f}{\delta t}}dx.}$

Сумарна зміна дає нам формулу Лейбніца.

• Weisstein, Eric W. Інтегральне правило Лейбніца(англ.) на сайті Wolfram MathWorld.