Алгоритм Ву
Алгоритм Ву — алгоритм для малювання ліній зі згладжуванням, був представлений в статті Ефективна техніка згладжування у липневому випуску видання Computer Graphics, а також в статті Швидке згладжування в червні 1992 в випуску Dr. Dobb's Journal.
Алгоритм Брезенхейма малює відрізок дуже швидко, але він не виконує згладжування. В додаток, він не може обробити ситуацію коли кінцеві точки мають не цілочисельні координати. Наївна спроба малювання зі згладжуванням вимагає багато часу, в той час як алгоритм Ву дуже швидкий (хоча й повільніший за алгоритм Брезенхейма).
Алгоритм
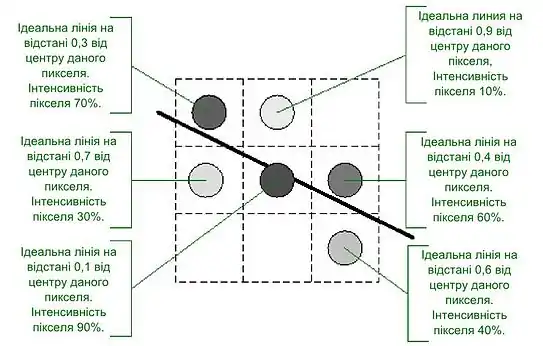
Горизонтальні та вертикальні лінії не вимагають ніякого згладжування, через це їх малювання виконується окремо. Для решти ліній алгоритм Ву проходить їх уздовж основної осі, підбираючи координати за неосновною віссю аналогічно з алгоритмом Брезенхейма. Відмінність складається в тому, що в алгоритмі Ву на кожному кроці встановлюється не одна, а дві точки. Наприклад, якщо основної віссю є Х, тоді розглядаються точки з координатами (х, у) і (х, у+1). В залежності від величини похибки, яка вказує як далеко відійшли піксели від ідеальної лінії за неосновною віссю, розподіляється інтенсивність між цими двома точками. Чим більше віддалена точка від ідеальної лінії, тим менша її інтенсивність. Значення інтенсивності двох пікселів завжди в сумі дає одиницю, тобто це є інтенсивність одного піксела, який точно потрапив на ідеальну лінію. Таке розподілення придасть лінії однакову інтенсивність по всій її довжині, створюючи при цьому ілюзію, що точки розташовані уздовж лінії не по дві, а по одній.
function plot(x, y, c) is
plot the pixel at (x, y) with brightness c (where 0 ≤ c ≤ 1)
function ipart(x) is
return integer part of x
function round(x) is
return ipart(x + 0.5)
function fpart(x) is
return fractional part of x
function rfpart(x) is
return 1 - fpart(x)
function drawLine(x1,y1,x2,y2) is
dx = x2 - x1
dy = y2 - y1
if abs(dx) < abs(dy) then
swap x1, y1
swap x2, y2
swap dx, dy
end if
if x2 < x1
swap x1, x2
swap y1, y2
end if
gradient = dy / dx
// handle first endpoint
xend = round(x1)
yend = y1 + gradient * (xend - x1)
xgap = rfpart(x1 + 0.5)
xpxl1 = xend // this will be used in the main loop
ypxl1 = ipart(yend)
plot(xpxl1, ypxl1, rfpart(yend) * xgap)
plot(xpxl1, ypxl1 + 1, fpart(yend) * xgap)
intery = yend + gradient // first y-intersection for the main loop
// handle second endpoint
xend = round (x2)
yend = y2 + gradient * (xend - x2)
xgap = fpart(x2 + 0.5)
xpxl2 = xend // this will be used in the main loop
ypxl2 = ipart (yend)
plot (xpxl2, ypxl2, rfpart (yend) * xgap)
plot (xpxl2, ypxl2 + 1, fpart (yend) * xgap)
// main loop
for x from xpxl1 + 1 to xpxl2 - 1 do
plot (x, ipart (intery), rfpart (intery))
plot (x, ipart (intery) + 1, fpart (intery))
intery = intery + gradient
end function
Зауваження: Якщо на початку виявляється, що abs(dx) < abs(dy), тоді всі точки мають відображатись з переставленими x і y.
Література
- Майкл Абраш (червень 1992). Швидке згладжування. Dr. Dobb's Journal 17 (6): 139(7). Архів оригіналу за 1 березня 2010. Процитовано 31 липня 2010.
- Ву Сяолінь (липень 1991). Ефективна техніка згладжування. Computer Graphics 25 (4): 143–152. ISBN 0-89791-436-8.