Алгоритм Дойча — Йожи
Алгоритм Дойча — Йожи (іноді алгоритм Дойча — Джози, англ. Deutsch–Jozsa algorithm) — квантовий алгоритм, запропонований Девідом Дойчем і Річардом Йожею в 1992 році[1] й вдосконалений Річардом Клівом, Артуром Екертом, К'ярою Маккіавелло й Мішелем Моска в 1998 році[2]. Цей алгоритм став одним із перших прикладів алгоритму для квантового комп'ютера. Завдяки використанню квантової переплутаності й принципу суперпозиції такий алгоритм має значний приріст швидкості виконання в порівнянні з відповідним класичним аналогом.
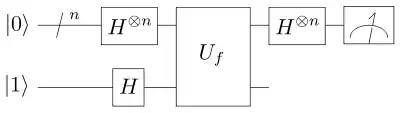
Задача Дойча — Йожи полягає у визначенні, чи є функція двійкової змінної константою (тобто, набуває або значення 0, або значення 1 за будь-яких аргументів) або збалансованою (для половини області визначення набуває значення 1, для іншої половини — значення 0). При цьому вважається, що функція a priori є або константою, або збалансованою.
Для розв'язання цієї задачі класичний детермінований алгоритм має виконати в найгіршому випадку обчислень функції . Класичний детермінований алгоритм потребує меншого часу, щоб дати правильну відповідь із високою ймовірністю. Але в будь-якому разі для отримання правильної відповіді з одиничною ймовірністю потрібно виконати обчислень. Алгоритм Дойча — Йожи завжди дає правильну відповідь, виконуючи лише одне обчислення функції .
Якщо функція незбалансована, то алгоритм може дати відповідь «константа» з деякою ймовірністю, причому при збільшенні різниці між кількістю «0» і «1» збільшується й ця ймовірність[3].
Алгоритм Дойча — Йожи оснований на схожому алгоритмі (алгоритм Дойча, розроблений Девідом Дойчем у 1985 році), який є частковим випадком першого. В цьому алгоритмі функція є функцією однієї змінної, на відміну від функції багатьох змінних , яка використовується в алгоритмі Дойча — Йожи.
Алгоритм Дойча — Йожи
На вході алгоритму маємо (n+1)-кубітовий стан . Тобто, останній кубіт знаходиться в стані , а інші n кубітів — стані . До кожного кубіту застосовується оператор Адамара для отримання стану:
Функція в алгоритмі грає роль квантового оракула, який перетворює стан на стан . Звертання до оракула призводить до наступної зміни стану:
- .
Оскільки для кожного функція дорівнює або 0, або 1, то вираз для стану спрощується:
- .
Після цього кроку останній кубіт, який є допоміжним, можна відкинути. До кожного з n кубітів, що залишилися, знову застосовується оператор Адамара, який змінює стан так:
де — побітовий добуток.
Зрештою, вимірюючи стан , отримуємо на виході алгоритму ймовірність
яка дорівнює 1, якщо функція — константа, і 0, якщо вона збалансована.
Алгоритм Дойча
Алгоритм Дойча — це частковий випадок алгоритму Дойча — Йожи: тепер функція є функцією однієї змінної. Задачею цього алгоритму є перевірка умови . Або, що те ж саме, обчислення (де — операція додавання за модулем 2, яка може бути представлена вентилем CNOT): якщо цей вираз дорівнює 0, то — константа.
На вході алгоритму маємо двокубітний стан . До кожного з кубітів застосовується оператор Адамара, що призводить до зміни стану:
Як і в минулому випадку грає роль квантового оракула, який змінює стан на . Звертання до оракула дає:
Відкидаючи другий (допоміжний) кубіт і фазу , загострюємо увагу на стані
до якого знову застосовується оператор Адамара:
Тепер можна виконати вимірювання стану першого кубіта. Легко бачити, що якщо вимірювання дає 0, то , тобто функція є константою. Якщо ж вимірювання дає 1, то , і функція є збалансованою.
Виноски
- Deutsch D., Jozsa R. Rapid solutions of problems by quantum computation // Proceedings of the Royal Society of London A. — 1992. — Т. 439. — С. 553. (рос. переклад: Дойч Д., Джозса Р. Быстрое решение задач с помощью квантовых вычислений // Квантовый компьютер и квантовые вычисления (том II). — Ижевск : РХД, 1999. — 288 с.)
- Cleve R., Ekert A., Macchiavello C., Mosca M. Quantum algorithms revisited // Proceedings of the Royal Society of London A. — 1998. — Т. 454. — С. 339-354.
- Вялый М. Квантовые алгоритмы (Лекция 2).
Література
- Кайе Ф., Лафламм Р., Моска М. Введение в квантовые вычисления. — Ижевск : РХД, 2009. — 360 с.
- Нильсен М., Чанг И. Квантовые вычисления и квантовая информация. — М. : Мир, 2006. — 824 с.
Див. також
- Квантовий алгоритм
- Квантовий комп'ютер