Алгоритм Рамера — Дугласа — Пекера

Алгоритм Рамера-Дугласа-Пекера — алгоритм, що дозволяє зменшити число точок кривої, апроксимованої більшою серією точок. Алгоритм було незалежно відкрито Урсом Рамером в 1972 та Давидом Дугласом і Томасом Пекером в 1973 та декількома іншими дослідниками протягом наступного десятиліття.[1] Також алгоритм відомий під назвами: алгоритм Дугласа-Пекера, алгоритм ітеративної найближчої точки та алгоритм розбиття і злиття.

Ідея

Суть алгоритму полягає в тому, щоб за даною ламаною, яка апроксимує криву, побудувати ламану з меншою кількістю точок. Алгоритм визначає розбіжність, яка обчислюється за максимальною відстанню між вихідною і спрощеною кривими. Спрощена крива складається з підмножини точок, які визначаються з початкової кривої.

Алгоритм
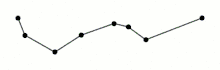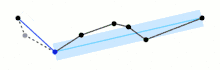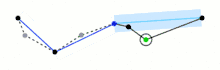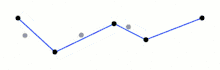
Згладжування кусково-лінійної кривої алгоритмом Дугласа-Пекера.
Згладжування кусково-лінійної кривої алгоритмом Дугласа-Пекера залежно вiд параметра ε.

Початкова крива являє собою упорядкований набір точок або ліній, і задану відстань ε > 0. Початкова крива показана на малюнку 0, спрощена — на малюнку 4.

Алгоритм рекурсивно ділить лінію. Входом алгоритму служать координати всіх точок між першою і останньою. Перша і остання точка зберігаються незмінними. Після чого алгоритм знаходить точку, найбільш віддалену від відрізка, що з'єднує першу і останню. Якщо точка знаходиться на відстані, меншій ε, то всі точки, які ще не були відзначені до збереження, можуть бути викинуті з набору і отримана пряма згладжує криву з точністю не нижче ε

Якщо ж відстань більше ε, то алгоритм рекурсивно викликає себе на наборі від початкової до даної і від даної до кінцевої точках (що означає, що дана точка буде відзначена до збереження). По закінченню всіх рекурсивних викликів вихідна ламана будується тільки з тих точок, що були відзначені до збереження.

Псевдокод (рекурсивна реалізація)

 
function DouglasPeucker(PointList[], epsilon)
 // Знаходимо точку з максимальною відстанню від прямої між першою й останньою точками набору
 dmax = 0
 index = 0
 for i = 2 to (length(PointList) - 1)
  d = PerpendicularDistance(PointList[i], Line(PointList[1], PointList[end])) 
  if d > dmax
   index = i
   dmax = d
  end
 end
 
 // Якщо максимальна дистанція більша, ніж epsilon, то рекурсивно викликаємо функцію на ділянках
 if dmax >= epsilon
  //Recursive call
  recResults1[] = DouglasPeucker(PointList[1...index], epsilon)
  recResults2[] = DouglasPeucker(PointList[index...end], epsilon)
  
  // Будуємо підсумковий набір точок
  ResultList[] = {recResults1[1...end-1] recResults2[1...end]}
 else
  ResultList[] = {PointList[1], PointList[end]}
 end
 
 // Повертаємо результат
 return ResultList[]
end

Псевдокод (ітеративна реалізація)

 
function DouglasPeucker(PointList[], epsilon)
{
 //  У стек заносимо перший і останній індекси
 stack.push({0, length(PointList) - 1})
 
 //  У масиві за заданим індексом зберігаємо точку (true) або ні (false) 
 keep_point[0...length(PointList) - 1] = true
 
 while(!stack.empty())
 {
   startIndex = stack.top().first
   endIndex = stack.top().second
   stack.pop()
   
   dMax = 0
   index = startIndex
   for(i = startIndex + 1 to endIndex - 1)
   {
      if(keep_point[i])
      {
         d = PerpendicularDistance(PointList[i], Line(PointList[startIndex], PointList[endIndex])) 
         if(d > dMax)
         {
           index = i
           dMax = d
         }
       }
    }
     
    if(dMax >= epsilon)
    {
       stack.push({startIndex, index})
       stack.push({index, endIndex})
    }
    else
    {
       for(j = startIndex + 1 to endIndex - 1)
       {
           keep_point[j] = false
       }
    }
 }
  
 for(i = 0 to (length(PointList) - 1))
 {
    if(keep_point[i])
    {
       ResultList.Add(PointList[i])
    }
 }
  
 return ResultList[]
}

Застосування

Алгоритм застосовується для обробки векторної графіки та при картографічній генералізації.

Крім того, застосовується у робототехніці[2] для обробки результатів роботи кругового лазерного далекоміру і тому також називається алгоритмом розбиття і злиття.

Складність

Очікувана складність алгоритму може бути оцінена виразом , яка спрощується (як наслідок основної теореми про рекурентні співвідношення) в . Проте в гіршому випадку складність алгоритму .

Примітки
  1. Heckbert, Paul S.; Garland, Michael (1997). Survey of polygonal simplification algorithms. с. 4.
  2. Nguyen and Martinelli and Siegwart (2005). A Comparison of Line Extraction Algorithms using 2D Laser Rangefinder for Indoor Mobile Robotics. Архів оригіналу за 17 вересня 2010. Процитовано 15 червня 2016.

Література


This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.