Гамільтонів граф
Гамільто́нів гра́ф — в математиці це граф, що містить гамільтонів цикл.
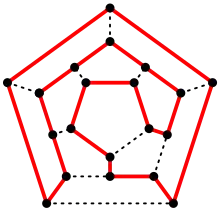
Гамільто́нів шля́х — шлях, що містить кожну вершину графу рівно один раз. Гамільтонів шлях, початкова і кінцева вершини якого збігаються, називається гамільтоновим циклом.
Гамільтонові шлях, цикл і граф названі на честь ірландського математика Вільяма Гамільтона, який вперше визначив ці класи, дослідивши задачу «навколосвітньої подорожі» по додекаедру, вузлові вершини якого символізували найбільші міста Землі, а ребра — дороги, що їх з'єднують.
Задачу знаходження гамільтонового циклу можна використати як основу для доведення з нульовим пізнанням.
Умови існування
Умова Дірака (1952)
Нехай — число вершин в даному графі; якщо степінь кожної вершини не менший, ніж , то граф називається графом Дірака. Граф Дірака — гамільтонів.
Умова Оре (1960)
— число вершин у даному графі. Якщо для будь-якої пари несуміжних вершин , виконано нерівність то граф називаваєтся графом Оре (словами: сума степенів будь-яких двох несуміжних вершин не менша від загального числа вершин у графі). Граф Оре — гамільтонів.
Умова Бонді-Хватала
Теорема Бонді-Хватала узагальнює твердження Дірака і Оре. Спочатку визначимо замикання графу. Нехай у графу є вершин. Тоді замикання однозначно будується за G додаванням для всіх несуміжних вершин і , у яких виконується , нового ребра .
Граф є гамільтоновим тоді і тільки тоді, коли його замикання — гамільтонів граф.
Приклади
- Будь-який повний граф є гамільтоновим.
- Усі цикли є гамільтоновими графами.
- Усі правильні багатогранники є гамільтоновими графами.
Див. також
- Гамільтонове доповнення
- Гіпотеза Ловаса про гамільтонів цикл
Джерела
- Bollobás, B. Graph Theory: An Introductory Course. New York: Springer-Verlag, 1979.
- Chartrand, G. Introductory Graph Theory. New York: Dover, 1985.