Декартове дерево

Декартове дерево (англ. Cartesian tree) — це двійкове дерево отримане з послідовності чисел; його можна однозначно побудувати якщо дотримуватись властивостей що воно впорядковане як купа і що центрований (in-order) обхід дерева повертає оригінальну послідовність. Вперше описане Вілеміном[1] в контексті структур даних для геометричного пошуку за областю, декартові дерева також використовувались у визначенні таких структур даних для двійкового пошуку як treap та рандомізоване двійкове дерево пошуку. Декартове дерево послідовності можна побудувати за лінійний час використовуючи стековий алгоритм для знаходження всіх найближчих менших значень в послідовності.

Послідовність значень і декартове дерево яке їй відповідає.

Означення

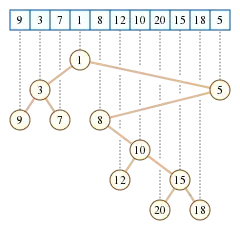
Декартове дерево послідовності різних чисел можна унікальним чином означити наступними властивостями:

  1. Декартове дерево послідовності має один вузол для кожного числа в послідовності. Кожен вузол дерева пов'язаний з єдиним елементом послідовності.
  1. Центрований (in-order) обхід дерева дає в результаті оригінальну послідовність. Тобто, ліве піддерево містить значення що зустрічаються в послідовності раніше за значення в корені дерева, а праве — значення що йдуть після кореня, і така ж умова виконується для кожного вузла.
  2. Дерево має властивість купи: предок будь-якого не кореневого вузла містить менше значення ніж той вузол. (Іноді порядок перевертають, так що предок містить більше значення, а корінь — максимальне).

Див. також

Зноски
  1. Vuillemin, 1980.

Література
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.