Зв'язуючий нейрон
Зв'язуючий нейрон (ЗН) — концепція обробки сигналів в нейроні загального типу і/або математична модель (моделі), яка втілює цю концепцію.
Опис концепції
Для нейрону загального типу стимулами є збуджуючі імпульси. Як правило, для збудження нейрону до рівня, коли він стріляє і посилає вихідний імпульс, потрібно більше ніж один вхідний. Нехай нейрон одержує вхідних імпульсів в послідовні моменти часу . В концепції ЗН вводиться поняття часової когерентності, , між вхідними імпульсами:
Висока часова когерентність між вхідними імпульсами свідчить на користь того, що в зовнішньому до нейрона середовищі всі імпульсів можуть бути породжені одною комплексною подією. Відповідно, ЗН, стимульований достатньо когерентним в часі набором імпульсів, стріляє і посилає вихідний імпульс. В термінології ЗН це називається зв'язуванням елементарних подій (вхідних імпульсів) в єдину подію. Зв'язування реалізується, якщо набір стимулюючих імпульсів характеризується достатньою часовою когерентністю і не реалізується, якщо когерентність вхідних імпульсів низька.
Гальмування в концепції ЗН (в першу чергу мається на увазі повільне соматичне калієве гальмування) контролює рівень часової когерентності між вхідними імпульсами, необхідний для зв'язування їх в єдину подію: чим вищий рівень гальмування, тим більша часова когерентність необхідна для зв'язування.

Вихідний імпульс вважається абстрактним представленням комплексної події (набору когерентних в часі вхідних імпульсів), див. Схему.
Походження
«Хоча нейрон і споживає енергію, його головна функція — одержувати сигнали і посилати їх назовні, отже — обробляти інформацію» — ці слова Френсіса Кріка вказують на потребу описати функцію поодинокого нейрона в термінах обробки абстрактних сигналів.[1] Існують дві абстрактні концепції функціонування нейрона, «детектор збігів» і «часовий інтегратор»,[2],[3]. В першій з них припускається, що нейрон збуджується і надсилає вихідний імпульс, якщо певна кількість вхідних імпульсів надходить до нього одночасно. В концепції часового інтегратора припускається, що нейрон збуджується і надсилає вихідний імпульс після того як одержує певну кількість вхідних імпульсів розподілених в часі. Кожна з цих концепцій враховує певні риси функціонування реальних нейронів, оскільки відомо, що функціонування конкретного нейрона може бути подібним до детектора збігів, або до часового інтегратора в залежності від характеру стимулів,[4]. Разом з тим відомо, що нейрони одержують крім збуджувальних імпульсів також і гальмівну стимуляцію. Природним розвитком згаданих вище двох концепцій мала б бути концепція, яка надає гальмуванню власну роль при обробці сигналів.
В той же час в нейронауках існує таке поняття, як зв’язування ознак і/або подій. Наприклад, при зоровому сприйнятті такі ознаки, як форма, колір і просторове розташування зорового об'єкту представлені в мозку в різних групах нейронів. Механізм, який забезпечує сприйняття сукупності цих ознак як приналежних одному реальному об'єкту, називається зв'язуванням ознак, [5]. Існує експериментально підтверджена думка, що для функціонування механізму зв'язування необхідна точна координація часових моментів нервових імпульсів, що відповідають тим чи іншим ознакам, [6], [7], [8], [9], [10], [11]. Ця координація в основному вимагає, щоб сигнали про різні ознаки надходили до певних областей в мозку в межах певного часового вікна.
Концепція ЗН відтворює на рівні поодинокого нейрона вимоги, сформульовані раніше на рівні крупномасштабних нейронних мереж, котрі забезпечують функціонування механізму зв'язування. Формулювання концепції здійснено на основі аналізу знайденого чисельно відгуку рівнянь Ходжкіна-Хакслі на стимули, подібні до тих, які одержуються нейронами в реальних умовах, див. «Математичні реалізації», нижче.
Математичні реалізації
Модель Ходжкіна-Хакслі (Х-Х)
Модель Ходжкіна-Хакслі — фізіологічно обґрунтована модель нейрону, що оперує в термінах іонних струмів крізь мембрану нейрону і описує механізм генерації нейроном потенціалу дії.
У роботі[12] досліджувався чисельно відгук моделі Х-Х на стимули складені з великого числа збуджуючих імпульсів, моменти одержання яких розподілені випадковим чином в межах певного часового вікна :
Тут позначає величину збуджувального постсинаптичного потенціалу в момент часу , — момент одержання -того імпульсу, — повне число імпульсів. Числа — випадкові, розподілені рівномірно в інтервалі . Застосований до моделі Х-Х стимул одержувався наступним чином
де — ємність одиниці площі збудливої мембрани. Обчислювалась ймовірність збудження нейрона до генерації спайку в залежності від ширини вікна . Розглядались рівняння Х-Х з різними значеннями фіксованої калієвої провідності, для створення певного рівня гальмівного потенціалу. Одержані залежності, перераховані на величину, обернену до ширини вікна, , яка є аналогом часової когерентності імпульсів в стимулі, мають вигляд сходинки, причому положення сходинки регулюється величиною гальмування, див. Рис. 1. Такий характер залежностей дозволяє трактувати рівняння Х-Х як математичну реалізацію концепції ЗН.
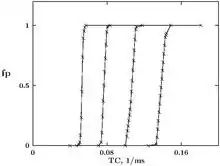
Інтегруючий нейрон з втратами (ІНВ)
Модель інтегруючого нейрону з втратами є широко розповсюдженою абстрактною моделлю нейрону. Якщо поставити аналогічну задачу для ІНВ, то при належним чином організованому гальмуванні сходинкоподібні залежності, аналогічні зображеним на Рис. 1, можна одержати і для ІНВ. Отже, ІНВ може служити математичною реалізацією концепції ЗН.
Модель «зв'язуючий нейрон»
Модель зв'язуючого нейрона реалізує концепцію ЗН в найбільш рафінованому вигляді. В цій моделі кожен вхідний імпульс зберігається в нейроні в незмінному вигляді протягом фіксованого часу після чого зникає. Нейрон характеризується пороговим значенням : якщо число наявних в нейроні імпульсів рівне, або більше від , то нейрон посилає вихідний імпульс і звільняється від наявних вхідних. Наявність гальмування в моделі ЗН реалізується як зменшення .
В моделі ЗН при обчисленні відгуку нейрона на потік вхідних імпульсів потрібно контролювати час, який залишилось провести в нейроні кожному присутньому в ньому імпульсу (час життя). Це робить модель ЗН при чисельному моделюванні більш складною ніж модель ІНВ, де потрібно контролювати тільки сумарне збудження. З іншого боку, кожен імпульс проводить в ЗН скінченний час після якого безслідно зникає. Це відрізняє модель ЗН від ІНВ, оскільки сліди вхідного імпульсу залишаються в ІНВ необмежено довго і зникають тільки в момент пострілу. Така властивість моделі ЗН дозволяє одержати точний опис статистики вихідної активності ЗН при стимуляції випадковим потоком імпульсів, див. [13] [14] [15].
Граничний випадок ЗН з нескінченною пам'яттю τ→∞ відповідає часовому інтегратору. Граничний випадок ЗН з нескінченно короткою пам'яттю τ→0 відповідає детектору збігів.
Мікросхемні реалізації
Перелічені вище та інші моделі нейронів і нейронні мережі з них мають свої реалізації на рівні електронних мікросхем. Серед застосованих мікросхем відмітимо програмовані користувачем вентильні матриці, ПКВМ. ПКВМ застосовуються для моделювання нейронів будь-яких типів, але найбільш природно в них реалізується модель ЗН, оскільки ця модель може бути реалізована без застосування чисел з плаваючою точкою і не потребує розв'язання диференціальних рівнянь. Ці особливості моделі ЗН використано, наприклад в [16] [17].
Обмеження
Концепція ЗН має низку обмежень, які випливають з її абстрактного характеру. До таких обмежень слід віднести ігнорування морфології нейронів, ідентичну інтенсивність вхідних імпульсів, заміну низки перехідних процесів з різними часами релаксації, які спостерігаються в реальних нейронах, єдиним часом життя імпульсу в нейроні, відсутність рефрактерного періоду, розгляд тільки повільного (калієвого) гальмування.
Такі ж обмеження має і модель ЗН, хоча частина з них може бути усунена за рахунок ускладнення моделі, див. наприклад [18], де використано модель ЗН з рефрактерним періодом і швидким гальмуванням.
Примітки
- F. Crick. The Astonishing Hypothesis. Touchstone., 1995.
- M. Abeles. Role of the cortical neuron: integrator or coincidence detector? Israel Journal of Medical Sciences, 18:83-92, 1982. PMID:6279540
- P. König, A. K. Engel, and W. Singer. Integrator or coincidence detector? the role of the cortical neuron revisited. Trends in Neurosciences, 19(4):130-137, 1996. http://dx.doi.org/10.1016/S0166-2236(96)80019-1 PMID:8658595
- M. Rudolph and A. Destexhe. Tuning neocortical pyramidal neurons between integrators and coincidence detectors. Journal of Computational.Neuroscience, 14(3):239-251, 2003. http://dx.doi.org/10.1023/A:1023245625896 PMID:12766426
- J. P. Sougné. Binding problem. In Encyclopedia of Cognitive Science. John Wiley & Sons, Ltd, 2006.
- A. M. Treisman and G. Gelade. A feature-integration theory of attention. Cognitive Psychology, 12:97-136, 1980. http://dx.doi.org/10.1016/0010-0285(80)90005-5 PMID:7351125
- von der C. Malsburg. The what and why of binding: The modeler's perspective. Neuron, 24(8):95-104, 1999. http://dx.doi.org/10.1016/S0896-6273(00)80825-9 PMID:10677030
- R. Eckhorn, R. Bauer, W. Jordan, M. Brosch, W. Kruse, M. Munk, and H. J. Reitboeck. Coherent oscillations: a mechanism for feature linking in the visual cortex? Biological Cybernetics, 60:121-130, 1988. http://dx.doi.org/10.1007/BF00202899 PMID:3228555
- A. R. Damasio. Concepts in the brain. Mind & Language, 4(1-2):25-28, 1989. http://dx.doi.org/10.1111/j.1468-0017.1989.tb00236.x
- A. K. Engel, P. König, A. K. Kreiter, C. M. Gray, and W. Singer. Temporal coding by coherent oscillations as a potential solution to the binding problem: physiological evidence. In H. G. Schuster and W. Singer, editors, Nonlinear Dynamics and Neuronal Networks, pages 325. VCH Weinheim, 1991.
- M. M. Merzenich, C. Schreiner, W. Jenkins, and X. Wang. Neural mechanisms underlying temporal integration, segmentation, and input sequence representation: some implications for the origin of learning disabilities. In P. Tallal, A. M. Galaburda, R. R. Llinás, and C. Von Euler, editors, Temporal Information Processing in the Nervous System, page 122. The New York Academy of Sciences, 1993. http://dx.doi.org/10.1111/j.1749-6632.1993.tb22955.x
- A. K. Vidybida. Neuron as time coherence discriminator. Biological Cybernetics, 74(6):537-542, 1996. http://dx.doi.org/10.1007/BF00209424 PMID:8672560
- О.К. Відибіда. Вихідний потік зв’язуючого нейрона. Український математичний журнал, 59(12):1619-1838, 2007, http://dx.doi.org/10.1007/s11253-008-0028-5
- A. K. Vidybida and K. G. Kravchuk. Delayed feedback makes neuronal firing statistics non-markovian. Ukrainian Mathematical Journal, 64(12):1587-1609, 2012, http://dx.doi.org/10.1007/s11253-013-0753-2
- Arunachalam, V., Akhavan-Tabatabaei, R., Lopez, C. Results on a Binding Neuron Model and Their Implications for Modified Hourglass Model for Neuronal Network. Computational and Mathematical Methods in Medicine, vol. 2013, Article ID 374878, 2013, http://dx.doi.org/10.1155/2013/374878
- J. L. Rosselló, V. Canals, A. Morro, and A. Oliver. Hardware implementation of stochastic spiking neural networks. International Journal of Neural Systems, 22(4):1250014, 2012. http://dx.doi.org/10.1142/S0129065712500141
- R. Wang, G. Cohen, K. M. Stiefel, T. J. Hamilton, J. Tapson, and A. van Schaik. An fpga implementation of a polychronous spiking neural network with delay adaptation. Frontiers in Neuroscience, 7(14), 2013. http://dx.doi.org/10.3389/fnins.2013.00014 PMID:23408739
- K. G. Kravchuk and A. K. Vidybida. Non-markovian spiking statistics of a neuron with delayed feedback in presence of refractoriness. Mathematical Biosciences and Engineering, 11(1):81-104, 2014. http://dx.doi.org/10.3934/mbe.2014.11.81
Посилання
- Стаття написана з використанням матеріалу публікації: Vidybida, A. (2014). Binding neuron. У Mehdi Khosrow-Pour. Encyclopedia of information science and technology (англ.) (вид. Third Edition) (Hershey PA: IGI Global): 1123—1134.