Колесна факторизація

З огляду на основу перших кількох простих чисел {2, 3, 5}, «перший оберт» колеса буде містити числа:

7, 11, 13, 17, 19, 23, 29, 31.

Другий оберт можна отримати шляхом додавання 30, добутку чисел основи, до чисел на першому оберті. Третій оберт отримують шляхом додавання 30 до другого оберта тощо.

Для реалізації методу можна зауважити, що приріст між двома послідовними елементами колеса, тобто

inc = [4, 2, 4, 2, 4, 6, 2, 6],

залишаються однаковими після кожного оберту.

Пропонована нижче реалізація використовує допоміжну функцію div(n, k), яка перевіряє, чи n ділиться на k без остачі, і повертає true у цьому випадку, false в іншому випадку. У цій реалізації число, яке підлягає факторизації, дорівнює n, і програма повертає найменший дільник n .

 тест: = хибний
якщо div ( n, 2) = true, то поверніть 2;
якщо div ( n, 3) = true, то поверніть 3;
якщо div ( n, 5) = true, то поверніть 5;
к   : = 7; i   : = 1
а тест = хибний і k * k ≤ n робити
  тест   : = div ( n, k )
  якщо тест = вірно, поверніть k
  к   : = k + inc [ i ]
  якщо i <8, то i   : = i + 1 інший i   : = 1
повернути n . 

Щоб отримати повну факторизацію цілого числа, обчислення можна продовжити без перезавантаження колеса на початку. Це призводить до наступної програми для повної факторизації, де функція add додає свій перший аргумент в кінці другого аргументу, що має бути списком.

 чинників   : = [];
while div ( n, 2) = true тоді
  чинники: = додати (2, фактори);
  н   : = п / 2;
while div ( n, 3) = true тоді
  фактори: = додати (3, фактори);
  н   : = п / 3;
while div ( n, 5) = true тоді
  чинники: = додати (5, фактори);
  н   : = п / 5;
к   : = 7; i   : = 1
а k * k ≤ n робити
  якщо div ( n, k ) = true тоді 
   додати ( k, фактори)
   н   : = п / к
  ще
   к   : = k + inc [ i ]
   якщо i <8, то i   : = i + 1 інший i   : = 1
повернути додавання ( n, факторів) 

Колесна факторизація використовується для генерування списків переважно простих чисел із простої математичної формули та значно меншого списку перших простих чисел. Ці списки можуть бути використані в пробному відділенні або ситах . Оскільки не всі числа в цих списках є простими, це вводить неефективні зайві операції. Однак самим генераторам потрібно дуже мало пам'яті в порівнянні з тим, щоб зберігати чистий список простих чисел. Невеликий список початкових простих чисел складають цілісні параметри алгоритму для генерації залишку списку. Ці генератори називають колесами . Незважаючи на те, що кожне колесо може генерувати нескінченний перелік чисел, в певний момент числа перестають бути переважно простими.

Спосіб може додатково застосовуватися рекурсивно як сіткове колесо основного числа для отримання більш точних коліс. Пол Прітчард[1][2][3][4] провів сформування ряду різних алгоритмів багато остаточної роботи щодо факторизації коліс, сит, що використовують колісну факторизацію, і колісне сито. Щоб візуалізувати використання колеса факторизації, можна почати з написання натуральних чисел навколо кіл, як показано на сусідній діаграмі. Кількість спиць вибирається такою, що прості числа будуть накопичуватися в меншості спиць.

1. Знайти перші кілька простих чисел, які ляжуть в основу колеса факторизації. Вони є відомими або, можливо, визначені з попередніх застосувань коліс меншої факторизації або шляхом швидкого пошуку їх за допомогою сита Ератостена .
2. Перемножити базові прості числа, щоб отримати результат n, який буде утворювати коло колеса факторизації.
3. Записати числа від 1 до n по колу. Це буде найбільше внутрішнє коло, що представляє одне обертання колеса.
4. Від чисел від 1 до n у самому внутрішньому колі викреслити усі кратні базові прості числа з першого кроку, як це зроблено на кроці 2. Це усунення складених чисел можна здійснити або за допомогою сита, такого як сито Ератостена, або як результат застосування коліс меншої факторизації.
5. Взявши x за кількість написаних кіл, продовжити писати xn + 1 до xn + n в концентричних колах навколо самого внутрішнього кола, таких, що xn + 1 знаходиться в тому ж положенні, що і (x − 1)n + 1.
6. Повторити крок 5 до тих пір, поки найбільше коло обертання не охопить найбільшу кількість тестування на простоту.
7. Закресліть число 1.
8. Відкресліть спиці простих чисел, як показано на кроці 1, і застосуйте на кроці 2 у всіх зовнішніх колах, не відкреслюючи прості числа у самому внутрішньому колі (у колі 1).
9. Відкресліть спиці всіх кратних простих чисел, вибитих із внутрішнього кола 1 на кроці 4 таким же чином, як відкреслити спиці базових праймерів на кроці 8.
10. Решта числа в колесі — це переважно прості числа (їх у сукупності називають «відносно» простими). Використовуйте інші методи, такі як сито Ератосфена або подальше застосування круглих коліс для факторизації, щоб видалити залишки, що не залишилися.

Колесна факторизація для основи n = 2x3 = 6

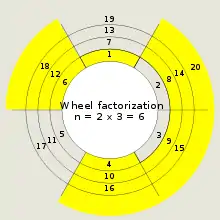
1. Визначаються перші два прості числа: 2 і 3.

2. n = 2 × 3 = 6

3.

 1 2 3 4 5 6 

4. Викреслюються числа, що діляться на числа основи: 4 і 6:

 1 2 3 4 5 6 

5. х = 1. xn + 1 = 1 · 6 + 1 = 7. (x + 1) n = (1 + 1) · 6 = 12. Записуються числа від 7 до 12 починаючи з 7:

 1 2 3 4 5 6
 7 8 9 10 11 12 

6. х = 2. xn + 1 = 2 · 6 + 1 = 13. (x + 1) n = (2 + 1) · 6 = 18. Виписуються числа від 13 до18 та повторюються наступні рядки:

 1 2 3 4 5 6
 7 8 9 10 11 12
13 14 15 16 17 18
19 20 21 22 23 24
25 26 27 28 29 30 

7 і 8. Просіювання:

 1 2 3 4 5 6
 7 8 9 10 11 12
13 14 15 16 17 18
19 20 21 22 23 24
25 26 27 28 29 30 

9. Просіювання

 1 2 3 4 5 6
 7 8 9 10 11 12
13 14 15 16 17 18
19 20 21 22 23 24
25 26 27 28 29 30 

10. Отриманий список містить непросте число 25, яке є повним квадратом числа 5. Необхідно виикористати інші методи, такі як сито, щоб позбутися нього в остаточному списку

 2 3 5 7 11 13 17 19 23 29 

Зауважимо, що, використовуючи точно наступне просте число з 5 циклів коліс та виключаючи кращі (і) цього простих (і тільки цього простих) із отриманого списку, ми отримали базове колесо, як на кроці 4, для колеса факторизації з базою простих чисел 2, 3 і 5; це одне колесо до попереднього 2/3 колеса факторизації. Потім можна виконати кроки до кроку 10, використовуючи наступний наступний простір 7 циклів і виключивши лише кратні 7 із результуючого списку на етапі 10 (залишаючи в цьому випадку деякі «відносні» прості числа та всі послідовні випадки — тобто деякі не відповідають дійсності повністю кваліфікований прості), щоб отримати наступне подальше вдосконалене колесо, рекурсивно повторюючи кроки в міру необхідності для отримання послідовно більших коліс.

Формально метод використовує наступні припущення: по-перше, набір базових простих чисел, об'єднаних з його (нескінченним) набором копійм, є надмножиною простих чисел; по-друге, нескінченний набір копрімесів можна легко перерахувати від копій до базового набору між 2 та базовим набором добутку. (Зверніть увагу, що 1 вимагає спеціального поводження.)

Як видно з наведеного вище прикладу, результатом повторних застосувань вищевказаної рекурсивної процедури від кроків 4 до 10 може бути список коліс, який охоплює будь-який бажаний діапазон просіювання (до якого він може бути усічений), а отриманий список потім включає лише кратні простих чисел, що перевищує останні минулі базові прайми.

Зауважте, що коли колесо проходить бажану верхню межу діапазону просіювання, можна зупинити генерування подальших коліс і використовувати інформацію на цьому колесі для скидання решти складених номерів із цього останнього списку коліс, використовуючи техніку типу «Сито Ератостена», але використовуючи проміжок візерунок, притаманний колесо, щоб уникнути зайвих скибочок; деякі оптимізації можуть бути здійснені виходячи з того, що (буде доведено в наступному розділі), що не буде повторного відсікання будь-якого складеного числа: кожен залишився композит буде викреслений рівно один раз. Крім того, можна продовжувати генерувати усічені списки коліс, використовуючи праймери до квадратного кореня потрібного діапазону сит, і в цьому випадку всі решти представлених чисел у колесі будуть простими; однак, хоча цей метод настільки ефективний, що ніколи не відкидати складені числа більше одного разу, він втрачає багато часу поза звичайно розглянутими операціями відсікання при обробці послідовних зачисток колеса, щоб зайняти набагато більше часу. Усунення складених чисел за допомогою колеса факторизації засноване на наступному: З огляду на число k> n, ми знаємо, що k не є простим, якщо k mod n і n не є відносно простими. З цього можна визначити частку чисел, яку усуває ситове колесо (хоча не всі потрібно фізично вражати; багато хто може автоматично сбиватися при операціях копіювання менших коліс на більші колеса) як 1 — phi (n) / n, що також є ефективністю сита.

Відомо, що

${\displaystyle \lim \inf {\frac {\varphi (n)}{n}}\log \log n=e^{-\gamma }\sim 0.56145948,}$

де γ — константа Ейлера. Таким чином, phi (n) / n повільно йде до нуля, оскільки n збільшується до нескінченності, і видно, що ця ефективність дуже повільно підвищується до 100 % для нескінченно великого n. З властивостей phi легко видно, що найефективніше сито менше x — це те, де ${\displaystyle n=p_{1}p_{2}...p_{i}<x}$і ${\displaystyle np_{i+1}\geq x}$ (тобто генерація колеса може зупинитися, коли пройде останнє колесо або має достатню окружність, щоб включити найбільшу кількість в діапазон просіювання).

Щоб максимально використати на комп'ютері, ми хочемо, щоб числа були меншими за n і відносно простими для нього у вигляді набору. Використовуючи декілька спостережень, безліч можна легко створити :

1. Починати з ${\displaystyle S_{1}=\{1\}}$, для якого встановлено ${\displaystyle n=1}$ з 2 як перше просте число. Цей початковий набір означає, що всі числа, що починаються з двох та вгору, включаються як «відносні» прості числа, оскільки окружність колеса дорівнює 1.
2. Наступні набори є ${\displaystyle S_{2}=\{1\}}$ що означає, що вона починається з 3 для всіх непарних чисел з усуненими множниками 2 (окружність 2),${\displaystyle S_{6}=\{1,5\}}$має усунені фактори 2 та 3 (окружність 6), як для початкового базового колеса у наведеному вище прикладі тощо.
3. Нехай ${\displaystyle S_{n}+k}$ буде множина, де k було додано до кожного елемента ${\displaystyle S_{n}}$.
4. Потім ${\displaystyle S_{np_{i+1}}=F_{p_{i+1}}[S_{n}\cup S_{n}+n\cup S_{n}+2n\cup ...\cup S_{n}+n(p_{i+1}-1)]}$ де ${\displaystyle F_{x}}$являє собою операцію видалення всіх кратних x.
5. 1 та ${\displaystyle p_{i+1}}$ будуть дві найменші з ${\displaystyle S_{n}}$ коли ${\displaystyle n>2}$ усуваючи необхідність окремо обчислювати прості числа, хоча алгоритм повинен вести облік всіх усунених базових простих чисел, які більше не включаються до наступних наборів.
6. Усі множини, де окружність n > 2 aповторно симетричні навколповторно симетричні навколо${\displaystyle n/2}$, зниження вимог до зберігання. Наступний алгоритм не використовує цей факт, але він ґрунтується на тому, що проміжки між послідовними числами в кожному наборі симетричні навколо половини точки шляху.

• Решето Ератосфена
• Решето Сундарама

• Wheel factorization
• Paul Pritchard (May 1994). Improved Incremental Prime Number Sieves. Proceedings of the First International Symposium on Algorithmic Number Theory. ANTS-I (Springer-Verlag): 280—288.