Мережа процесів Кана

Мережа процесів Кана (мережа процесів, мережа потоків даних) — це розподілена модель обчислень, в якій група детермінованих процесів взаємодіє через необмежені канали FIFO. Мережі процесів володіють детермінованою поведінкою, яка не залежить від обчислювальних і комунікаційних затримок. Спочатку розроблені для моделювання розподілених систем, мережі процесів виявилися ефективні також для моделювання систем обробки сигналів. Моделлю обчислень є орієнтований граф, вершини якого є обчислювальними процесами, а дуги — впорядкованими послідовностями елементів даних. Обчислювальні процеси постійно здійснюють обробку вхідних даних, породжуючи набори вихідних даних. Назва даної моделі пов'язана з тим, що мережі процесів були вперше описані Жілем Каном.[1]

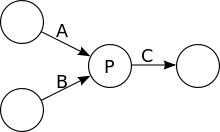
Мережа Кана з трьох процесів без зворотної комунікації. Ребра A, B і C — комунікаційні канали, P — один з процесів.

Модель виконання

KPN — загальна модель для опису систем обробки сигналу, де безкінечні потоки даних зі зростанням перетворюють процеси, що виконуються один за іншим або паралельно. Не дивлячись на паралельні процеси, багатозадачність або паралелізм не потрібні для виконання цієї моделі.

У KPN, процеси зв'язуються через безмежні канали FIFO. Процеси зчитують і пишуть атомні елементи даних, або альтернативно називаються знаками, від і до каналів. Запис до каналу є безперебійним, тобто це завжди має успіх і не зупиняє процес, поки читання з каналу є заблокованим, тобто процес, який читає з порожнього каналу, зупиниться і може продовжуватися, коли канал містить достатні елементи даних (знаки).

Процеси не дозволяють перевірити вхідний канал на існування знаків без вжитку їх. FIFO не можуть спожити багаторазові процеси, також не може відбутися багаторазове відтворення процесів в єдиний FIFO. Отримали специфічну вхідну (знак) історію для процесу, процес має бути детермінований таким чином, що це завжди відтворює, ту ж саму продуктивність (знаки). Розрахунок часу або замовлення виконання процесів не повинне впливати на результат і тому перевірка вхідних каналів для знаків заборонено.

Відмітки на процесах
  • Процесу не потрібно зчитувати будь-які вхідні дані або мати будь-які вхідні канали, оскільки це, можливо, служить джерелом постійних даних
  • Процесу не потрібно писати будь-які вихідні дані або мати будь-які вихідні канали
  • Вхідні канали тестування для порожнечі (або безперебійного зчитування) може дозволятися для цілей оптимізації, але це не повинно зачіпати вихідні канал. Це може бути вигідне і/або можливо зробити що-небудь заздалегідь замість чекання для каналу. Наприклад, можна припустити, що було 2 зчитування з різних каналів. Якби перше зчитування зупинилось (дочекайтеся знаку) але друге зчитування могло зчитати знак безпосередньо, може бути вигідно зчитувати другий, щоб економити час, тому що, зчитування себе часто споживає деякий час (наприклад час для розміщення пам'яті або копіювання). 

Процес звільнення семантики, як мереж Петрі
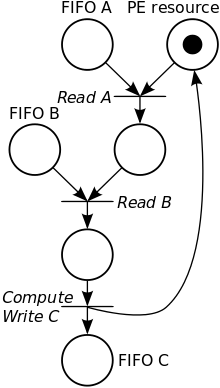
Firing semantics of process P modeled with a Petri net displayed in the image above

Припустимо, що процес P в KPN сконструйований таким чином, що він спершу читає дані з каналу А, потім канал B, обчислює що-небудь, а потім пише дані, щоб направити C, модель виконання процесу може моделюватися з мережею Петрі. Єдиний знак в PE місці ресурсу забороняє, виконання процесу одночасно для різних початкових даних. Коли дані прибувають в канал А або B, знаки розміщуються на місця FIFO А і FIFO B відповідно. Переміщення мережі Петрі асоційовані з відповідними діями I/O і обчисленнями. Коли дані був записані до каналу C, ресурс PE наповнюється його початковою маркіровкою знову, дозволяючи новим даним бути зчитаними.

Процес як закінчений апарат
A finite state machine of a process

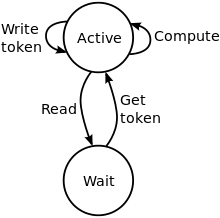
Процес може моделюватися як закінчений апарат, який знаходиться в одному із двох станів:

  • Активний; процес обчислює або пише дані 
  • В очікуванні; процес блокується (в очікуванні) для даних 

Припустимо, що закінчений апарат зчитує елементи програми, що асоціюються з процесом, і може, прочитати три види знаків: «Обчислюють», «Читаються» і знак «Запису». Додатково, в стані Очікування можливо лише повернутися до Активного стану, зчитаючи спеціальний «Отримуючий знак», який означає, що канал зв'язку, що асоціюється з чеканням, містить чіткі дані.

Властивості

Необмежена кількість каналів

Канал строго обмежує {\displaystyle b} b, якщо це має як мінімум {\displaystyle b} b не реалізовані знаки для будь-якого можливого виконання. KPN строго обмежує {\displaystyle b} b, якщо всі канали строго обмежують {\displaystyle b} b.

Число не реалізованих знаків залежить від замовлення (планування) виконання процесів. Мимовільне джерело даних могло виробляти довільно багато знаків в каналі, якщо планувальник не зможе виконати процеси, використовуючи ті знаки.

Реальне застосування не обмежує FIFOs і тому планування і максимальна місткість FIFOs повинна проектуватися в практичному виконанні. Максимальна місткість FIFOs може управлятися декількома способами:

  • Обмеження FIFO можуть бути математично отримані в проекті, щоб уникати надлишків FIFO. Проте це не можливо для всього KPNs. Це — нерозв'язна проблема, щоб перевірити чи KPN строго обмежує{\displaystyle b} b. Окрім того, в практичних ситуаціях, обмеження, можливо, є утриманням даних.[джерело?]
  • Обмеження FIFO можуть бути побудовані за вимогою (запитом).[2]
  • Блокування записів може бути використане таким чином, процес блокується, якщо FIFO повний. Цей підхід, на жаль, приводить до штучної безвихідності, якби тільки проектувальник належним чином отримав безпечні обмеження для FIFOs (Parks, 1995). Місцеве штучне виявлення в часі виконання, можливо, необхідне, щоб гарантувати виробництво правильного вихідного каналу (вихідних даних).
    [3]

Закриті (замкнуті) та відкриті системи

Закритий KPN не має жодних зовнішніх вхідних або вихідних каналів. Процеси, що не мають жодного вхідного каналу, діють як джерела даних і процеси, що не мають жодного вихідного каналу, діють як приймачі даних. У відкритому KPN кожен процес має як мінімум один вхідний і вихідний канал.

Детермінізм

Процеси KPN детерміновані. Для тієї ж вхідної історії вони повинні завжди виробляти точно такі самі вихідні. Процеси можуть моделюватися як послідовні програми, які зчитуються і пишуться для портів в будь-якому порядку або кількості, поки властивість детермінізму збережена. Як наслідок, модель KPN детермінована таким чином, що наступні чинники повністю визначають вихідні системи:

  • процеси
  • мережі
  • початкові знаки

Віднині, розрахунок часу процесів не зачіпає вихідні системи.

Монотонність

Процеси KPN монотонні, це означає, що їм лише потрібна часткова інформація вхідного потоку для того, щоб виробляти часткову інформацію вихідного потоку. Монотонність дозволяє паралелізм. У KPN є повна почерговість подій усередині сигналу. Проте, немає жодного чергування зв'язків між подіями в різних сигналах. Тому, KPNs лише частково впорядковані, це класифікує їх як нехронометровану модель.

Додатки

Завдяки його високій виразності і стислості, KPNs, який лежить в основі моделі обчислення застосовується в декількох академічних моделюючих інструментах, щоб представити поточні додатки, які мають певні властивості (наприклад, орієнтованість на потік даних, поточність).

Відкрита вихідна структура Daedalus, підтримувана Лейден, заснувала Центр Досліджень в Лейденському Університеті, і прийняла послідовні програми, написані на C, і виробляє відповідний KPN. Це KPN зміг, наприклад, бути використаним, щоб нанести на карту KPN, на заснованій FPGA- платформі систематично.

Ambric Am2045 в широкому масштабі паралельний масив процесора — KPN, здійснюваний у кремнії.[4] Тут 336 32-розрядних процесорів сполучено програмованим сполучним дротом відданого FIFOs. Тому його канали строго обмежують блокування записів.

Примітки
  1. Kahn, G. (1974). У Rosenfeld, Jack L. The semantics of a simple language for parallel programming Proc. IFIP Congress on Information Processing. North-Holland. ISBN 0-7204-2803-3.
  2. Parks, Thomas M. (1995). Bounded Scheduling of Process Networks (Ph. D.). University of California, Berkeley.
  3. Geilen, Marc; Basten, Twan (2003). У Degano, P. Requirements on the Execution of Kahn Process Networks Proc. 12th European Symposium on Programming Languages and Systems (ESOP). Springer. с. 319–334.
  4. Mike Butts, Anthony Mark Jones, Paul Wasson, «A Structural Object Programming Model, Architecture, Chip and Tools for Reconfigurable Computing», Proceedings of FCCM, April 2007, IEEE Computer Society

Подальше читання
  • Lee, E.A.; Parks, T.M. (1995). Dataflow process networks. Proceedings of the IEEE 83 (5): 773–801. ISSN 00189219. doi:10.1109/5.381846. Процитовано 13 лютого 2019.
  • Josephs, Mark B. (2005). Models for Data-Flow Sequential Processes. У Ali E. Abdallah, Cliff B. Jones, Jeff W. Sanders (eds.). Communicating Sequential Processes. The First 25 Years: Symposium on the Occasion of 25 Years of CSP, London, UK, July 7-8, 2004. Revised Invited Papers. Lecture Notes in Computer Science 3525. Berlin, Heidelberg: Springer Berlin Heidelberg. с. 85–97. ISBN 978-3-540-32265-8. doi:10.1007/11423348_6.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.