Метод Гука — Дживса

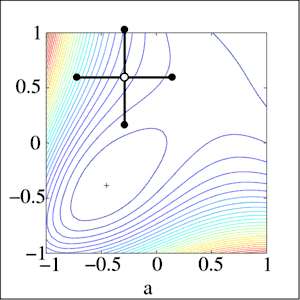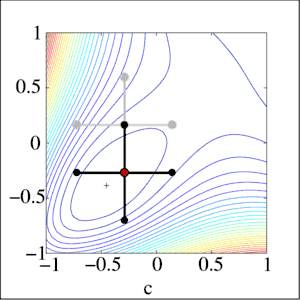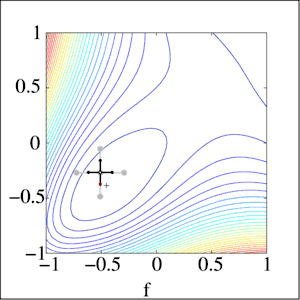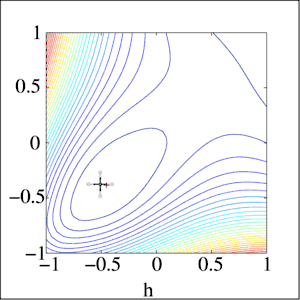
На початковому етапі задається стартова точка (позначимо її 1) і кроки h_i по координатах. Потім заморожуємо значення всіх координат крім 1-ї, обчислюємо значення функції в точках x₀+h₀ і x₀-h₀ (де x₀ — перша координата точки, а h₀ — значення кроку по цій координаті) і переходимо в точку з найменшим значенням функції. У цій точці заморожуємо значення всіх координат крім 2-ї, обчислюємо значення функції в точках x₁+h₁ i x₁-h₁, переходимо в точку з найменшим значенням функції і т. д. для всіх координат. У випадку, якщо для будь-якої координати значення у вихідній точці менше, ніж значення для обох напрямків кроку, то крок по цій координаті зменшується. Коли кроки по всіх координатах h_i стануть менше відповідних значень e_i, алгоритм завершується, і точка 1 визнається точкою мінімуму.

Ілюстрація першого етапу для двох координат:

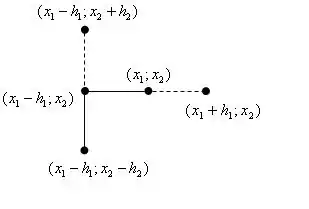
Таким чином, провівши досліджуючий пошук по всіх координатах, ми отримаємо нову точку з найменшим значенням функції в околі (позначимо її 2). Тепер можна перейти до 2 фази алгоритму.

На етапі пошуку за зразком відкладається точка 3 в напрямку від 1 до 2 на тій же відстані. Її координати знаходять за формулою ${\displaystyle {\overline {x}}_{3}={\overline {x}}_{1}+\lambda ({\overline {x}}_{2}-{\overline {x}}_{1})}$, де x_i — точка з номером i, λ — параметр алгоритму, зазвичай вибирають рівним 2. Потім в новій точці 3 проводиться досліджуючий пошук, як на першій фазі алгоритму, за винятком того, що крок не зменшується. Якщо на цій фазі в результаті досліджуючого пошуку вдалося отримати точку 4, відмінну від точки 3, то точку 2 позначимо як 1, а 4 як 2 і повторимо пошук за зразком. Якщо не вдається знайти точку 4, відмінну від точки 3, то точку 2 позначимо як точку 1 і повторимо першу фазу алгоритму — досліджуючий пошук.

Ілюстрація другого етапу для двох координат:

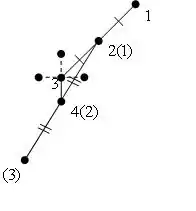
У дужках зазначені імена точок після перевизначення. На ілюстрації добре помітно, як алгоритм коригує свій напрямок в залежності від знайдених значень функції.

Даний алгоритм володіє властивістю «прискорюватися», що сприяє підвищенню його загальної ефективності. Друга перевага методу Гука—Дживса — можливість отримання за його допомогою наближеного рішення, якість якого безупинно підвищується на всіх стадіях чисельного рішення. Особливо явно переваги подібних засобів виявляються при відшуканні екстремумів на гіперповерхнях, які містять глибокі вузькі западини, тобто тоді, коли градієнтні методи неефективні. Також перевагами даного методу є проста стратегія пошуку і невеликий обсяг необхідної пам'яті.

Алгоритм заснований на циклічному русі по координатам, що може привести до виродження алгоритму в нескінченну послідовність пошуків через дослідження без пошуку за зразком. При використанні методу передбачається, що цільова функція яка досліджується, є унімодальною, тобто має на інтервалі дослідження тільки один оптимум. Це означає, що розв'язком може стати локальний мінімум, а не глобальний, якщо на досліджуваній області присутні кілька мінімумів.

1. Р. Гук, Т. А. Дживс «Прямой поиск решения для числовых и статических проблем», 212—219 с., 1961.
2. C. T. Kelley. Iterative methods for optimization, 180 p

• https://web.archive.org/web/20120905151449/http://www.theweman.info/topics/t4r5part1.html
• Методы многомерное оптимизации в Интуит.ру.
• А.В. Аттетков, С.В. Галкин, В.С. Зарубин. {{{Заголовок}}}.^{[недоступне посилання з квітня 2019]}