Метод скінченних різниць в часовій області

Ме́тод скінче́нних різни́ць у часові́й о́бласті (англ. Finite Difference Time Domain, FDTD) — один з найпопулярніших методів числової електродинаміки, який базується на дискретизації рівнянь Максвелла, записаних у диференціальній формі.

Опис

FDTD відноситься до загального класу сіткових методів розв'язку диференціальних рівнянь. Базовий алгоритм методу був вперше запропонований Кейном Йі (Каліфорнійський університет) в 1966 р. в статті «Numerical solution of initial boundary value problems involving maxwell’s equations in isotropic media» журналу «IEEE Transactions on Antennas and Propagation»[1]. однак, назва «Finite-difference time-domain» та абревіатура FDTD були дані методу Аленом Тафловим (Північно-західний університет, штат Іллійнойс).

В первісному вузькому сенсі під FDTD малось на увазі використання базового алгоритму Йі для числового розв'язку рівнянь Максвела. В сучасному більш широкому сенсі FDTD включає в себе безліч найрізноманітніших можливостей: моделювання середовищ з дисперсійними і нелінійними властивостями, застосування різних типів сіток (окрім, первинно запропонованої прямокутної сітки Йі), використання методів постпроцесорної обробки результатів і т.д.

Приблизно з 1990 р. метод скінченних різниць став основним для моделювання найрізноманітніших оптичних застосунків. Він може з успіхом бути застосованим для розв'язку широкого спектра задач: від моделювання наддовгих електромагнітних хвиль в геофізиці (включно з процесами в іоносфері) та мікрохвиль (наприклад, для вивчення сигнатурної радіолокації, розрахунку характеристик антен, розробки безпровідних пристроїв зв'язку, в тому числі цифрових) до розв'язку задач в оптичному діапазоні (фотонний кристал, наноплазматика, солитони і біофотоніка). До 2006 р. кількість публікацій, присвячених FDTD, досягла двох тисяч.

На даний момент існує близько 30 комерційних програм FDTD, а також проекти з відкритим вихідним кодом.

Алгоритм Йі

В рівняннях Максвела зміна електричного поля E (часткова похідна) залежить від розподілу в просторі магнітного поля H (ротор). Аналогічно, зміна поля H залежить від розподілу в просторі поля E.

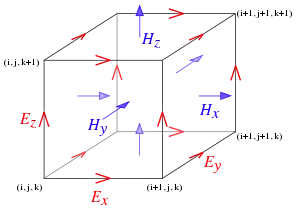
Поля в комірці сітки FDTD. Такі комірки становлять просторову тривимірну сітку Йі.

На цьому спостереженні базується алгоритм Йі. Сітки полів E та H по відношенню один до одного на половину кроку дискретизації часу і по кожній з просторових змінних. Кінцево-різницеві рівняння дозволяють визначити поля E та H на даному часовому кроці на основі відомих значень полів на попередньому.

При заданих початкових умовах алгоритм Йі дає еволюційний розв'язок в часі від початку відліку зі заданим часовим кроком.

Аналогічна сітка використовується при розв'язку задач гідродинаміки (для тиску і поля швидкості).

Як в будь-якому іншому різницевому методі, в FDTD існує проблема неточного відображення границі тіла на обчислювальну сітку. Будь-яка крива поверхня, яка розділяє з'єднані середовища і геометрично неузгоджені з сіткою, буде спотворюватись ефектом "ступінчастого наближення". Для вирішення даної проблеми можна використовувати додаткову сітку з великою роздільною здатністю в тих областях простору, де розташовані тіла зі складною геометричною структурою[2]. Також можна видозмінювати різницеві рівняння у вузлах сітки, які знаходяться поблизу границі між сусідніми тілами[3]. Менш затратним методом є введення ефективної діелектричної проникності поблизу границі між тілами (subpixel smoothing)[4][5].

Чисельна схема FDTD не передбачає можливості табличного задання залежності діелектричної проникності від частоти. Однак, її можна представити у вигляді апроксимації членами Дебая, Друде, Лоренца чи Лоренца з поглинанням. Така апроксимація не обов'язково має фізичний зміст і може бути отримана чисельно, наприклад за допомогою програми[6].

Поглинаючі граничні умови
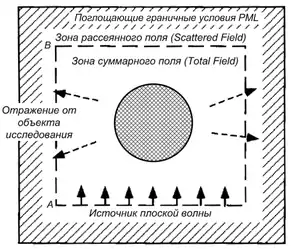
Генерація плоскої хвилі в двовимірному просторі, який має поглинаючі граничні умови PML

Для того, щоб обмежити об'єм сітки, в FDTD потрібні особливі поглинаючі граничні умови, які модулюють вихід електромагнітної хвилі на нескінченість.

Для цього використовуються поглинаючі граничні умови Мура чи Ляо[7], або ідеально узгоджені шари (Perfect Matched Layers, PML). Умови Мура чи Ляо набагато простіші, ніж PML. Проте, PML, які, строго кажучи, є поглинаючою приграничною областю, а не граничною умовою як такою, дозволяють отримати на порядки менші за величиною коефіцієнти відбиття від границі.

Поняття ідеально узгоджених шарів (PML) було введено Жаном П'єром Беренже в статті журналу «The Journal of Computational Physics» у 1994 р.[8] Ідея PML базувалась на розбитті вихідних полів E та H на дві компоненти, для кожної з яких мають розв'язуватись свої рівняння. Згодом були запропоновані удосконалені формулювання PML еквівалентні первісному формулюванню Беренже. Так, в одноосьових PML (Uniaxial PML) використовується анізотропний поглинаючий матеріал, що дозволяє не вводити додаткові змінні і залишатись в рамках вихідних рівнянь Максвела[9]. Однак, одноосьові PML, як і PML у формулюванні Беренже, не зручні тим, що в них відсутнє поглинання затухаючих хвиль, що не дозволяє поміщати PML близько до розсіюючих тіл. Цього недоліку позбавлені конволюційні PML (Convolutional PML), які базуються на аналітичному продовженні рівнянь Максвела на комплексну площину таким чином, що їх розв'язок експоненціально затухає[10]. CPML також зручніші в обмеженні нескінченних провідних та дисперсних середовищ. Окрім цього, математичне формулювання CPML демонструє велику наочність і доступність для розуміння.

В деяких випадках використання PML приводить до розбіжності розрахунку FDTD. Цю проблему можна усунути шляхом поміщення за PML додаткової поглинаючої стінки[11].

Порядок розрахунку FDTD

Хід розрахунку FDTD виглядає наступним чином:

  • Задається область, в якій проводяться розрахунки, розподільна здатність сітки і граничні умови. Граничні умови можуть бути поглинаючими чи періодичними. Останні застосовуються для моделювання нормального падіння плоскої хвилі на періодичну структуру. Схема FDTD для моделювання падіння плоскої хвилі під кутом потребує періодичних умов зі зсувом по часу, які можуть бути реалізовані за допомогою різних методів[12][13][14].
  • Всередині області, в якій рахують поміщають матеріальні тіла зі заданими оптичним властивостями (діелектрична проникність і магнітна провідність)
  • Задається джерело. Найпростіший спосіб задання джерела полягає в заданні часової залежності щільності струму J в рівнянні Ампера. Такий тип джерела зазвичай використовується при моделюванні диполей. Для генерації плоскої хвилі більш зручний другий тип джерела, який реалізується за допомогою методу повного і розсіяного поля (Total Field / Scattered Field).
  • Джерело генерує кінцеву в часі електромагнітну хвилю, спектральний склад якої має покривати діапазон частот, які нас цікавлять. Далі, хвиля падає на тіла, перерозсіюється на них та, при наявності поглинаючих граничних умов, через якийсь час виходить з області, в якій проводяться розрахунки. Історія розповсюдження хвилі зберігається.
  • За допомогою перетворення Фур'є записані значення полів переводяться в частотне представлення. Далі, обробляючи їх (наприклад, інтегруючи потік енергії поля через будь-яку поверхню), можна отримати оптичні характеристики даної структури тіл. Використовуючи метод перетворення ближнього поля в далеке (Near to Far Transformation), можна отримати значення полів за межами області, в якій проводяться розрахунки, на підставі еволюції поля всередині цієї області[15].

Переваги та недоліки FDTD

Як і будь-який інший чисельний метод, FDTD має свої переваги і недоліки.

Переваги:

  • FDTD - це простий і інтуїтивно зрозумілий метод.
  • Оскільки FDTD працює в часовій області, він дозволяє отримати результат для широкого діапазону довжин хвиль за один розрахунок. Це може бути корисно при вирішенні завдань, в яких невідомі резонансні частоти, або в разі моделювання широкосмугових сигналів.
  • FDTD дозволяє створювати анімовані зображення поширення хвилі в об'ємі, яке моделюється.
  • FDTD зручний при описі анізотропних, дисперсних та нелінійних середовищ.
  • Метод дозволяє безпосередньо моделювати крайові ефекти і ефекти екранування, причому поля всередині і поза екраном можуть бути розраховані як напряму, так і ні.

Недоліки:

  • Величина кроку дискретизації по простору повинна бути значно менше досліджуваних довжин хвиль і типових розмірів досліджуваної структури. У деяких випадках (інверсні опали з маленькими перегородками між кульками) це може потребувати сіток з маленьким кроком, що означає великі витрати пам'яті і великий час розрахунку.
  • FDTD розраховує поля всередині розрахункової області. Якщо потрібно знайти поле на великій відстані від джерела, то необхідне збільшення області, в якій проводяться розрахунки, і часу розрахунку. Існують модифікації методу для знаходження поля на відстані, але вони вимагають попередньої обробки.

Джерела
  1. Kane Yee (1966). Numerical solution of initial boundary value problems involving Maxwell's equations in isotropic media. IEEE Transactions on Antennas and Propagation 14 (3): 302–307.
  2. S. S. Zivanovic, K. S. Yee, and K. K. Mei (1991). A subgridding method for the Time Domain Finite-Difference Method to solve Maxwell's equations. IEEE Trans. Microware Theory Tech. 38: 471.
  3. T. G. Jurgens, A. Taflove, K. Umashankar, and T. G. Moore (1992). Finite-difference time-domain modeling of curved surfaces. IEEE Trans. Antennas Propag. 40: 357.
  4. J. Nadobny, D. Sullivan, W. Wlodarczyk, P. Deuflhard, and P. Wust (2003). A 3-D tensor FDTD-formulation for treatment of sloped interfaces in electrically inhomogeneous media. IEEE Trans. Antennas Propag. 51: 1760.
  5. A. Deinega and I. Valuev (2007). Subpixel smoothing for conductive and dispersive media in the FDTD method. Opt. Lett. 32: 3429.
  6. Фитинг диэлектрической проницаемости. Архів оригіналу за 9 червня 2012. Процитовано 18 травня 2017.
  7. G. Mur (1981). Absorbing boundary conditions for the finite-difference approximation of the time-domain electromagnetic field equations. IEEE Transactions on Electromagnetic Compatibility 23 (4): 377–382.
  8. J. Berenger (1994). A perfectly matched layer for the absorption of electromagnetic waves. Journal of Computational Physics 114 (2): 185–200.
  9. S. D. Gedney (1996). An anisotropic perfectly matched layer absorbing media for the truncation of FDTD lattices. IEEE Transactions on Antennas and Propagation 44 (12): 1630–1639.
  10. J. A. Roden and S. D. Gedney (2000). Convolution PML (CPML): An efficient FDTD implementation of the CFS-PML for arbitrary media. Microwave and Optical Technology Letters 27 (5): 334–339.[недоступне посилання з квітня 2019]
  11. A. Deinega and I. Valuev (2011). Long-time behavior of PML absorbing boundaries for layered periodic structures. Comp. Phys. Comm. 182: 149.
  12. I. Valuev, A. Deinega, and S. Belousov (2008). Iterative technique for analysis of periodic structures at oblique incidence in the finite-difference time-domain method. Opt. Lett. 33: 1491.
  13. A. Aminian and Y. Rahmat-Samii (2006). Spectral FDTD: a novel technique for the analysis of oblique incident plane wave on periodic structures. IEEE Trans. Antennas and Propagation 54: 1818.
  14. J. A. Roden, S. D. Gedney, M. P. Kesler, J. G. Maloney, and P. H. Harms (1998). Time-domain analysis of periodic structures at oblique incidence: orthogonal and nonorthogonal FDTD implementations. Microwave Theory and Techniques 46: 420.
  15. K. R. Umashankar and A. Taflove (1982). A novel method to analyze electromagnetic scattering of complex objects. IEEE Transactions on Electromagnetic Compatibility 24 (4): 397–405.

Посилання
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.