Метод стрільби

Крайова задача лінійна, якщо f має форму

${\displaystyle f(t,y(t),y'(t))=p(t)y'(t)+q(t)y(t)+r(t).\,}$

В такому разі розв'язок крайової задачі зазвичай задає

${\displaystyle y(t)=y_{(1)}(t)+{\frac {y_{1}-y_{(1)}(t_{1})}{y_{(2)}(t_{1})}}y_{(2)}(t)}$

де ${\displaystyle y_{(1)}(t)}$ - розв'язок задачі початкових значень:

${\displaystyle y''(t)=f(t,y(t),y'(t)),\quad y(t_{0})=y_{0},\quad y'(t_{0})=0,}$

та ${\displaystyle y_{(2)}(t)}$ її розв'язок:

${\displaystyle y''(t)=p(t)y'(t)+q(t)y(t),\quad y(t_{0})=0,\quad y'(t_{0})=1.}$

Дивіться доведення для точних умов, при яких такий результат має місце.

Нехай дано систему (1) звичайних диференційних рівнянь II порядку виду:

${\displaystyle \left\{{\begin{matrix}{{dy_{1}(x)} \over dx}=f_{1}(x,y_{1},y_{2}),\,\,\,\,\,\,\,\,\,\,\,\,\,\,\ \\{{dy_{2}(x)} \over dx}=f_{2}(x,y_{1},y_{2}),\,\,\,\,\,\,\,\,\,(1)\\\end{matrix}}\right.}$

Необхідно знайти розв’язок системи (1) на інтервалі x ∈ [x₀;x_n], який задовольняє граничні умови

${\displaystyle \left\{{\begin{matrix}g_{1}(x_{0},y_{1}(x_{0}),y_{2}(x_{0}))=0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\ \\g_{2}(x_{n},y_{1}(x_{n}),y_{2}(x_{n}))=0,\,\,\,\,\,\,\,\,\,(2)\\\end{matrix}}\right.}$

Сутність методу - у зведенні граничної задачі до багаторазового розв'язання задачі Коші для заданої системи.

Припустимо, що

${\displaystyle y_{1}(x_{0})=a,\,\,\,\,\,\,\,\,\,(3)}$

де a - довільне число. Підставимо припущене a в першу граничну умову (2)

${\displaystyle g_{1}(x_{0},y_{1}(x_{0}),y_{2}(x_{0}))=0,\,\,\,\,\,\,\,\,\,(4)}$.

Тепер це співвідношення є рівнянням відносно однієї невідомої ${\displaystyle y_{2}(x_{0})}$. В результаті чисельного чи аналітичного його розв'язання, отримуємо

${\displaystyle y_{2}(x_{0},a)=b,\,\,\,\,\,\,\,\,\,(5)}$.

Таким чином, сформульовано задачу Коші для системи диференційних рівнянь (1) з початковими умовами (3) і (5) в точці x₀. Розв'язавши дану задачу, отримані з необхідною точністю значення функцій ${\displaystyle y_{1}(x_{n},a),\quad y_{2}(x_{n},a),}$ підставимо в другу граничну умову (2):

${\displaystyle g_{2}(x_{n},y_{1}(x_{n},a),y_{2}(x_{n},a))=0,\,\,\,\,\,\,\,\,\,(6)}$,

яка не буде виконуватись через довільність обраного a. Співвідношення (6) можна розглядати як рівняння відносно змінної а. Значення а = а^*, що є коренем цього рівняння, задовольняє усім граничним умовам (2). Отже, розв'язками поставленої задачі будуть функції ${\displaystyle y_{1}(x,a^{*}),\quad y_{2}(x,a^{*})}$.

Для знаходження розв'язку а^* рівняння (6) найчастіше використовують метод січних, алгоритм якого в конкретному випадку запишеться у вигляді:

${\displaystyle a_{i+1}=a_{i}-{{a_{i}-a_{i-1}} \over {g_{2}(a_{i})-g_{2}(a_{i-1})}}g_{2}(a_{i})}$,

де i - номер поточної ітерації.

Хай дана така крайова задача[1]:

${\displaystyle w''(t)={\frac {3}{2}}w^{2},\quad w(0)=4,\quad w(1)=1}$

Задача початкових значень:

${\displaystyle w''(t)={\frac {3}{2}}w^{2},\quad w(0)=4,\quad w'(0)=s}$

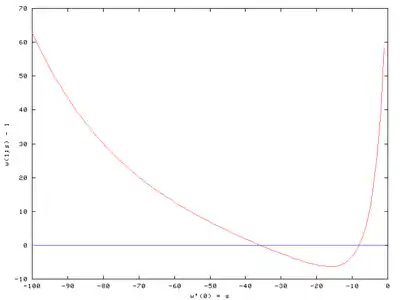
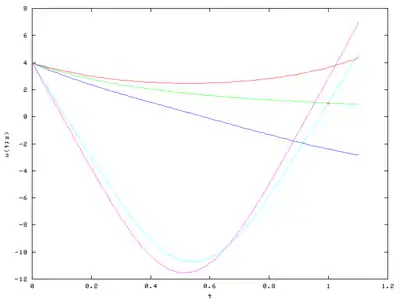
розв'язана для s = −1, −2, −3, ..., −100, і F(s) = w(1;s) − 1 була накреслена на першій ілюстрації. Досліджуючи графік F, ми бачимо, що є корені біля −8 та −36. Деякі траєкторії w(t;s) показані на другому малюнку.

Розв'язки задачі початкових значень були обчислені алгоритмом LSODE, який реалізований в математичному пакеті GNU Octave.

Автори задачі стверджують що існує два розв'язки, які можуть бути знайденими алгебраїчними методами. Вони відповідають початковим умовам w′(0) = −8 та w′(0) = −35.9 (приблизно).

Функція F(s) = w(1;s) − 1.

Траєкторії w(t;s) для ${\displaystyle s=w'(0)}$ що рівне −7, −8, −10, −36, та −40 (червоний, зелений, синій, голубий та рожевий кольори відповідно). Точка (1,1) позначена червоним ромбиком.

• Прямий мультиплікативний метод стрільби

• Josef Stoer and Roland Bulirsch. Introduction to Numerical Analysis. New York: Springer-Verlag, 1980. (See Section 7.3.)
• Мудров А.Е.. Численные методы для ПЭВМ на языках Бейсик, Фортран и Паскаль. Томск: МП"РАСКО", 1991. (Раздел 7.2)

1. Stoer and Bulirsch (Section 7.3.1).

• Shooting method - відео лекції. Університет Південної Флориди
• Brief Description of ODEPACK (at Netlib; contains LSODE)
• Shooting method of solving boundary value problems – Notes, PPT, Maple, Mathcad, Matlab, Mathematica at Holistic Numerical Methods Institute
• Shooting Method for Boundary Value Problems
• Boundary value problems: the shooting method