Теорема Мікеля

Теорема Мікеля — твердження в планіметрії, пов'язане з перетином трьох кіл, кожне з яких проходить через вершину трикутника і дві точки на прилеглих до неї сторонах. Названо на честь французького математика Огюста Мікеля[1]. Ця теорема — один з декількох отриманих Мікелем результатів, що стосуються кіл у геометрії, і опублікованих ним у Journal de mathématiques pures et appliquées.

Малюнок, на якому зображено три кола, що проходять через вершини трикутника

ABC

і точки

A'

,

B'

і

C'

, які лежать на сусідніх сторонах трикутника, і перетинаються у спільній точці M.

Теорема Мікеля для різних видів трикутників

Формулювання

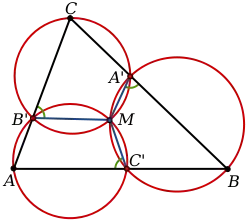
Нехай $ABC$ — трикутник із довільними точками $A'$ , $B'$ і $C'$ на сторонах $BC$ , $AC$ і $AB$ відповідно (або на їх продовженнях). Опишемо три кола навколо трикутників $AB'C'$ , $A'BC'$ , і $A'B'C.$ Теорема Мікеля стверджує, що ці три кола перетнуться в одній точці $M$ , яку називають точкою Мікеля. Окрім того, рівні будуть також кути $\angle MA'B,\angle MB'C,\angle MC'A$ (позначені на малюнку).[2][3]

Окремий випадок

Якщо точка Мікеля — центр описаного кола трикутника, а діаметри трьох кіл Мікеля дорівнюють радіусу описаного кола трикутника, і кожне з трьох кіл Мікеля проходить через спільну для них точку — центр описаного кола, а також через дві проєкції цього центра на сторони трикутника і через одну з трьох вершин, тоді радіуси трьох кіл Мікеля однакові.

Див. також

Точка Мікеля — інший результат Мікеля

Примітки

Ostermann та Wanner, (2012).
Miquel, Auguste (1838). Mémoire de Géométrie. Journal de Mathématiques Pures et Appliquées 1: 485–487.^{[недоступне посилання з квітня 2018]}
Wells, 1991 — Wells refers to Miquel's theorem as the pivot theorem

Література

Coxeter, H.S.M.; Greitzer, S.L. (1967). Geometry Revisited. New Mathematical Library 19. Washington, D.C.: Mathematical Association of America. ISBN 978-0-88385-619-2. Zbl 0166.16402.
Forder, H.G. (1960). Geometry. London: Hutchinson.
Ostermann, Alexander; Wanner, Gerhard (2012). Geometry by its History. Springer. ISBN 978-3-642-29162-3.
Pedoe, Dan (1988) [1970]. Geometry / A Comprehensive Course. Dover. ISBN 0-486-65812-0.
Smart, James R. (1997). Modern Geometries (вид. 5th). Brooks/Cole. ISBN 0-534-35188-3.
Wells, David (1991). The Penguin Dictionary of Curious and Interesting Geometry. New York: Penguin Books. ISBN 0-14-011813-6. Zbl 0856.00005.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[FOOTNOTEOstermannWanner2012-1] Ostermann та Wanner, (2012).

[2] Miquel, Auguste (1838). Mémoire de Géométrie. Journal de Mathématiques Pures et Appliquées 1: 485–487.^{[недоступне посилання з квітня 2018]}

[Wells-3] Wells, 1991 — Wells refers to Miquel's theorem as the pivot theorem