Тетраедр Ріва
У геометрії тетраедр Ріва — це багатогранник в тривимірному просторі з вершинами в точках , , і , де — натуральне число. Він названий на честь Джона Ріва, який використав його, щоб показати, що не існує багатовимірних узагальнень теореми Піка.
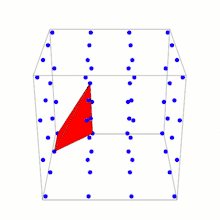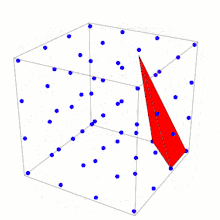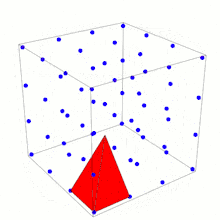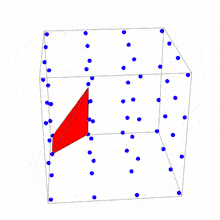
Контрприклад до узагальнення теореми Піка
Кожна вершина тетраедра Ріва лежить на фундаментальній точці гратки (точка в ℤ3). Жодна інша точка гратки не лежить на поверхні чи усередині тетраедра. Об'єм тетраедра Ріва — . У 1957 році Рів використав цей тетраедр, щоб показати, що існують тетраедри з чотирма точками гратки як вершинами і які не містять інших точок гратки, і при цьому мають значно більші об'єми.[1]
У двовимірному просторі площа кожного багатогранника з вершинами на гратки визначається за допомогою формули через кількості точок гратки у його вершинах, на гранях та всередині багатогранника відповідно до теореми Піка. Тетраедр Ріва показує, що не може бути відповідної формули об'єму в розмірності три і більше. Будь-яка така формула не змогла б відрізнити один від одного тетраедри Ріва з різними варіантами вибору , хоча їх об'єми різні.[1]
Рів показав, що попри негативний результат, можна отримати іншу формулу об'єму багатогранника через кількість точок гратки в багатограннику, кількість точок тоншої гратки в багатограннику та характеристику Ейлера для багатогранника.[1][2]
Многочлен Ергарта
Многочлен Ергарта для будь-якого багатогранника на ґратці визначає число точок ґратки, що він містить, при масштабуванні у натуральне число разів. Многочлен Ергарта для тетраедра Ріва висоти має вигляд:[3]
Таким чином, коефіцієнт при у многочлені Ергарта буде від'ємний, якщо . Цей приклад показує, що многочлени Ергарта іноді можуть мати від'ємні коефіцієнти.[3]
Література
- Reeve, J. E. (1957). On the volume of lattice polyhedra. Proceedings of the London Mathematical Society. Third Series 7: 378–395. doi:10.1112/plms/s3-7.1.378.
- Kołodziejczyk, Krzysztof (1996). An “odd” formula for the volume of three-dimensional lattice polyhedra. Geometriae Dedicata 61 (3): 271–278. doi:10.1007/BF00150027.
- Beck, Matthias; Robins, Sinai (2015). Computing the Continuous Discretely: Integer-Point Enumeration in Polyhedra. Undergraduate Texts in Mathematics (вид. Second). New York: Springer. pp. 78–79, 82. ISBN 978-1-4939-2968-9. doi:10.1007/978-1-4939-2969-6.