Частка в одновимірному періодичному потенціалі

У квантовій механіці, частка в одновимірному періодичному потенціалі це ідеалізована задача, яка може бути розв'язана точно (при деяких спеціального вигляду потенціалах), без спрощень. Припускається, що потенціал нескінченний та періодичний, тобто має трансляційну симетрію, що взагалі не виконується в реальних кристалах, де завжди існує як мінімум один дефект - поверхня (це приводить до іншої задачі про поверхневі стани або таммовські рівні).

Постановка задачі

Розглянемо одномірну решітку позитивних іонів, віддаль міє якими $\!a$ . Потенціал в цьому випадку буде виглядати подібно до цього:

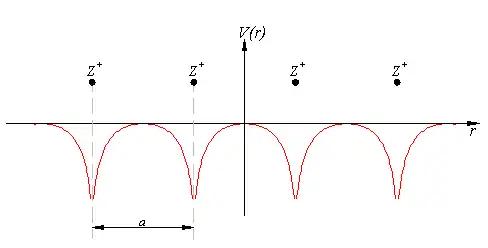
Рівняння Шредінгера в цьому випадку буде:

-{\frac {\hbar ^{2}}{2m}}{\frac {\partial ^{2}\psi (x)}{\partial x^{2}}}+V_{a}(x)\psi (x)=E\psi (x)

з періодичним потенціалом $V_{a}(x)=V_{a}(x+a).$ Загальний вигляд розв'язку рівняння Шредінгера з періодичним потенціалом, згідно з теоремою Блоха —

\psi (x)=e^{ikx}u(x),\;

де u(x) — деяка періодична функція:

u(x + a) = u(x).

k називають квазіімпульсом, за аналогією з хвильовою функцією e^ikx для частки з певним імпульсом k.

Як видно, вся хвильова функція визначається певною величиною k та будь-якою ділянкою функції довжиною a.

При наближенні до країв решітки появляється проблема граничних умов. Зручно представити решітку кільцем деякої довжини L >> a. Якщо L — довжина решітки така що L >> a, тоді число іонів в решітці настільки велике, що хвильові функції електрона в сусідніх іонів не розрізняються.

Тут замість двох граничних умов залишається тільки одне:

\psi (0)=\psi (L)\,

Якщо N — число іонів в решітці, то aN = L. Підставляючи хвильову функцію в граничну умову, получаємо квантування для k:

\psi (0)=e^{ik\cdot 0}u(0)=e^{ikL}u(L)=\psi (L)\,

u(0)=e^{ikL}u(Na)\rightarrow e^{ikL}=1\,

\Rightarrow kL=2\pi n\rightarrow k={2\pi  \over L}n\qquad \left(n=0,\pm 1,\pm 2,...,\pm {N \over 2}\right).\,

Модель Кроніга-Пенні

Для спрощення задачі використовують прямокутний потенціал:

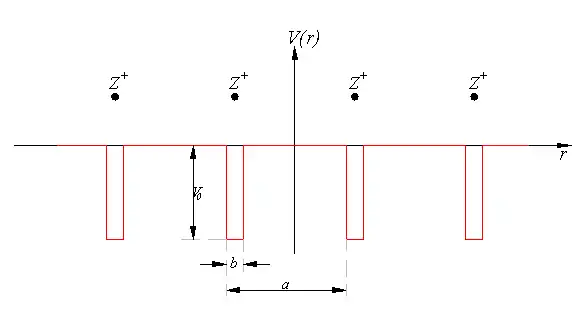
Використовуючи теорему Блоха можна знайти хвильову функцію у всьому просторі, проте спершу необхідно знайти розв'язок для одного періоду, та зробити його гладким на краях, тобто "зшити" значення сусідніх функцій та їхніх похідних.

Розглянемо один період потенціалу:

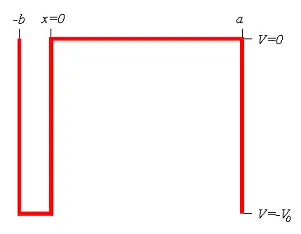
У нас є дві незалежні області для яких можна знайти розв'язки:

0<x<a-b:{-\hbar ^{2} \over 2m}\psi _{xx}=E\psi

\Rightarrow \psi =Ae^{i\alpha x}+A'e^{-i\alpha x}\quad \left(\alpha ^{2}={2mE \over \hbar ^{2}}\right)

-b<x<0:{-\hbar ^{2} \over 2m}\psi _{xx}=(E+V_{0})\psi

\Rightarrow \psi =Be^{i\beta x}+B'e^{-i\beta x}\quad \left(\beta ^{2}={2m(E+V_{0}) \over \hbar ^{2}}\right)

Для знаходження u(x) в кожній області необхідно зробити такі перетворення:

\psi (0<x<a-b)=Ae^{i\alpha x}+A'e^{-i\alpha x}=e^{ikx}\cdot \left(Ae^{i(\alpha -k)x}+A'e^{-i(\alpha +k)x}\right)

\Rightarrow u(0<x<a-b)=Ae^{i(\alpha -k)x}+A'e^{-i(\alpha +k)x}

Аналогічним чином отримуємо

u(-b<x<0)=Be^{i(\beta -k)x}+B'e^{-i(\beta +k)x}\;

Щоб знайти повний розв'язок необхідно впевнитися в гладкості функції на границях:

\psi (0^{-})=\psi (0^{+})\quad \psi '(0^{-})=\psi '(0^{+})

та періодичності u(x) u'(x)

u(-b)=u(a-b)\quad u'(-b)=u'(a-b).\,

Ці умови дають наступну матрицю:

{\begin{pmatrix}1&1&-1&-1\\\alpha &-\alpha &-\beta &\beta \\e^{i(\alpha -k)(a-b)}&e^{-i(\alpha +k)(a-b)}&-e^{-i(\beta -k)b}&-e^{i(\beta +k)b}\\(\alpha -k)e^{i(\alpha -k)(a-b)}&(\alpha +k)e^{-i(\alpha +k)(a-b)}&-(\beta -k)e^{-i(\beta -k)b}&(\beta +k)e^{i(\beta +k)b}\end{pmatrix}}{\begin{pmatrix}A\\A'\\B\\B'\end{pmatrix}}={\begin{pmatrix}0\\0\\0\\0\end{pmatrix}}

Для існування нетривіального розв'язку необхідно обнулення детермінанту цієї матриці. Після деяких перетворень отримуємо:

\cos(ka)=\cos(\beta b)\cos[\alpha (a-b)]-{\alpha ^{2}+\beta ^{2} \over 2\alpha \beta }\sin(\beta b)\sin[\alpha (a-b)].\qquad (*)

Для подальшого спрощення можна виконати такі спрощення, зміст яких полягає в переході до дельта-подібних потенціалів (гребінець Дірака) :

{\displaystyle b\rightarrow 0\

{\displaystyle \Rightarrow \beta b\rightarrow 0\

Тоді кінцевий результат буде:

\cos(ka)=\cos(\alpha a)-P{\sin(\alpha a) \over \alpha a}\qquad \left(P={\beta ^{2}ab \over 2}\right)

Програмний код

Код для Maple

Наступний програмний код написаний на мові Maple (9.5). Він є безпосередньо графічний розв'язок $(*)$ .

  restart;
  with(plots):
  with(stats[statplots]):
  eq:=cos(k*a)=cos(beta*b)*cos(alpha*(a-b)) - (alpha^2+beta^2)/(2*alpha*beta)*sin(beta*b)*sin(alpha*(a-b));
  alpha:=sqrt(8*Pi^2*m*(E)*e/h^2):
  beta:=sqrt(8*Pi^2*m*(E+V)*e/h^2):
  e:=1.6*1e-19:
  a:=0.54310*1e-9:
  m:=0.19*9.1*1e-31:
  b:=1/5*a:
  h:=6.6*1e-34:
  k(E,V):=arccos(rhs(evalf(eq)));

  #Графік
  p:=plot({subs(V=10,k(E,V)),subs(V=10,-k(E,V))},E=-5..50,labels=[ka, E],color=blue):
  xyexchange(p);

  #Анімація, залежність від глибини ями
  p:=animate( plot, [{k(E,V),-k(E,V)},E=-10..50, color=blue,labels=[ka, E]], V=0..30 ):
  xyexchange(p);

На малюнках подані графічні розв'язки рівняння ( * ).

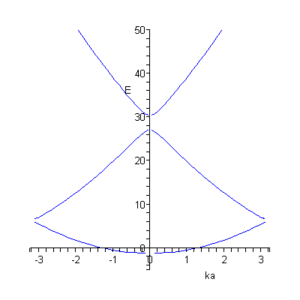Лінії відповідають дозволеним значенням енергії. Існують області енергії, при любих значеннях хвилевого вектора неможливе існування електрону.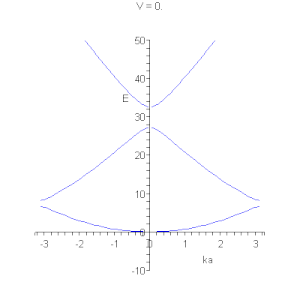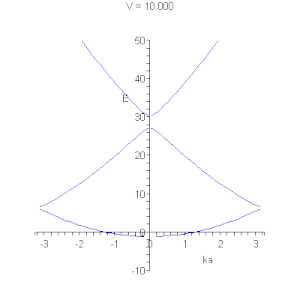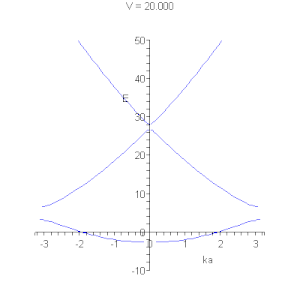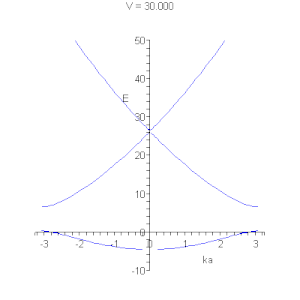

Лінії відповідають дозволеним значенням енергії. Показано рух закону дисперсії в залежності від глибини потенціальної ями.

На правому малюнку видно, як при деякому значенні потенційної енергії можливе утворення одновимірногобезщільового напівпровідника.

Код для Scilab

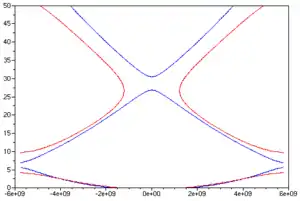
Ліеії иак само відповідають дозволеним значенням енергії. Синім позначено розв"язок для моделі Кроніга-Пенні, червоним - гребінця Дірака при тих же значеннях V₀b

Код нижче є фактично перекладом попередньої програми на мову Scilab, за тим виключенням, що ілюструє також і випадок переходу до гребінця Дірака.

clear all

global Pi e a m b h

Pi = 3.1415926;

step = 0.1;

e = 1.6 * 1e-19;
a = 0.54310 * 1e-9;
m = 0.19*9.1 * 1e-31;
b = 1/5 * a;
h = 6.6 * 1e-34;

function [alpha, beta] = ab(V,E)
  alpha = sqrt(8*Pi^2*m*(E)*e/h^2);
  beta  = sqrt(4*Pi^2*m*(E+V)*e/h^2);
endfunction

function r=kronigpenney(V, E)
  [alpha, beta] = ab(V,E);
  r = 1/a * acos((cos(beta*b) .* cos(alpha*(a-b)) ) - (alpha.^2+beta.^2) / (2*alpha .* beta) .* sin(beta*b) .* sin(alpha*(a-b)));
endfunction

function r=dirac(V,E)
  [alpha, beta] = ab(V,E);
  r = 1/a * acos(cos(alpha * a) - (beta.^2 * b * a) / 2 .* sin(alpha*a) / (alpha * a));
endfunction

E = [0 : step: 50];

k = kronigpenney(10, E);
plot(k, E, 'b'); plot(-k, E, 'b');

k = dirac(10, E);
plot(k, E, 'r'); plot(-k, E, 'r');

Посилання

Задачи по квантовой механике. Часть 1. Галицкий, Карнаков, Коган.
1-D periodic potential applet
Energy band formation

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.