RANSAC
RANSAC (абр. RANdom SAmple Consensus) це ітеративний метод, що використовується для оцінки параметрів математичної моделі для набору спостережуваних даних які містять викиди.
Це невизначений алгоритм, в тому сенсі, що він знаходить прийнятне рішення тільки з певною імовірністю, імовірність зростає відповідно до зростання кількості ітерацій. Алгоритм вперше був опублікований Fischler і Bolles в SRI International в 1981. Вони використовували алгоритм в задачах визначення положення (англ. Location Determination Problem, LDP), де головна задача — визначити положення точок у просторі, знаючи їхні проекції на площину зображення.
Алгоритм ґрунтується на припущенні, вихідні дані складаються з викидів і не-викидів. Не-викиди задовільняють математичну модель з певним набором параметрів, тоді як викиди є результатом шумів, і не задовільняють моделі. RANSAC також припускає, що існує процедура, яка по невеликому набору не-викидів може оцінити параметри моделі, що оптимально відповідає вхідним даним.
Приклад
Простим прикладом є знаходження лінії по набору точок для двовимірного випадку. Припускаючи, що набір даних складається з не-викидів — тобто точок, які приблизно можуть бути наближені прямою, і викидів — точок, що не можуть бути наближені прямою.
Якщо використовувати звичайний метод найменших квадратів якість наближення буде поганою. Причиною цьому є те, що метод буде намагатися підібрати коефіцієнти так, щоб задовольнити всім точкам включно з викидами. RANSAC з іншого боку, у випадку, якщо імовірність вибрати з набору даних тільки не-викиди достатньо висока, може створити модель, яка буде обчислена тільки на не-викидах.
Набір даних з великою кількістю викидів.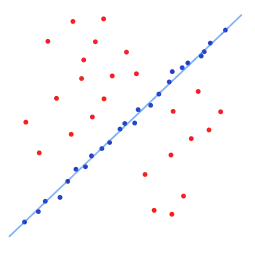
Лінія знайдена за допомогою алгоритму RANSAC; викиди не вплинули на результат.
Опис алгоритму
- Вибрати випадкову підмножину з вхідних даних. Назвемо її потенційні не-викиди.
- Підібрати параметри моделі для набору потенційних не-викидів.
- Всі інші точки перевіряються на приналежність до прямої. Точки які з деякою точністю належать до прямої назвемо набором погоджених точок.
- Модель вважається достатньо вдалою, якщо достатньо великий відсоток точок належить до набору погоджених точок.
- Далі модель може бути уточнена використовуючи всі точки з набору погоджених точок.
Ця операція проводиться певну кількість разів, як результат обираємо модель з найбільшим набором погоджених точок.
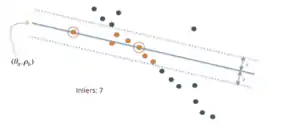RANSAC: викиди і не-викиди.
Реалізація у Matlab
Реалізація у Matlab для знаходженні лінії у 2D за допомогою алгоритму RANSAC:
function [bestParameter1,bestParameter2] = ransac_demo(data,num,iter,threshDist,inlierRatio)
% data: a 2xn dataset with #n data points
% num: the minimum number of points. For line fitting problem, num=2
% iter: the number of iterations
% threshDist: the threshold of the distances between points and the fitting line
% inlierRatio: the threshold of the numer of inliers
%% Plot the data points
figure;plot(data(1,:),data(2,:),'o');hold on;
number = size(data,2); % Total number of points
bestInNum = 0; % Best fitting line with largest number of inliers
bestParameter1=0;bestParameter2=0; % parameters for best fitting line
for i=1:iter
%% Randomly select 2 points
idx = randperm(number,num); sample = data(:,idx);
%% Compute the distances between all points with the fitting line
kLine = sample(:,2)-sample(:,1);
kLineNorm = kLine/norm(kLine);
normVector = [-kLineNorm(2),kLineNorm(1)];
distance = normVector*(data - repmat(sample(:,1),1,number));
%% Compute the inliers with distances smaller than the threshold
inlierIdx = find(abs(distance)<=threshDist);
inlierNum = length(inlierIdx);
%% Update the number of inliers and fitting model if better model is found
if inlierNum>=round(inlierRatio*number) && inlierNum>bestInNum
bestInNum = inlierNum;
parameter1 = (sample(2,2)-sample(2,1))/(sample(1,2)-sample(1,1));
parameter2 = sample(2,1)-parameter1*sample(1,1);
bestParameter1=parameter1; bestParameter2=parameter2;
end
end
%% Plot the best fitting line
xAxis = -number/2:number/2;
yAxis = bestParameter1*xAxis + bestParameter2;
plot(xAxis,yAxis,'r-','LineWidth',2);