Алгоритм Косараджу

Алгоритм Косараджу (англ. kosaraju algorithm) — алгоритм для знаходження компонент сильної зв’язності орієнтованого графу. Ахо, Хопкрофт і Ульман приписують його до неоприлюдненого паперу Косараджу від 1978. Він використовує факт, що транспонований граф (той самий граф з оберненими напрямками ребер) має ті самі компоненти сильної зв'язності, що й початковий граф.

Алгоритм Косараджу працює так:

Нехай G орієнтований граф і S порожній стек.
Допоки S не містить всі вершини:
- Вибрати довільну вершину v не з S. Виконати пошук в глибину від v. По завершені пошуку в глибину для кожної вершини u, заштовхуємо u на S.
Обернути всі ребра для отримання транспонованого графу.
Доки S непорожній (містить вершину в порядку завершення, на верхівці стеку — останнє завершення пошуку в глибину):
- Виштовхнути вершину v з S. Виконати пошук в глибину від v. Набір відвіданих вершин дасть компоненту сильної зв'язності, що містить v; записати це і видалити всі ці вершини з графу G і стеку S. Так само можна використати пошук в ширину.

Лема

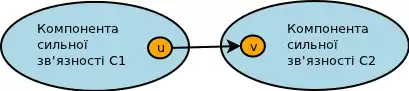
Розглянемо дві суміжні компоненти сильної зв'язності в G (зображення праворуч). Нехай f(v) — порядок завершення для вершини v в DFS-циклі. Тоді:

\max _{v\in C_{1}}f(v)>\max _{v\in C_{2}}f(v).

Доведення послуговується фактом, що мета-граф (ущільнений граф) такий, в якому всі компоненти сильної зв'язності стягнуті до однієї вершини є ациклічним.

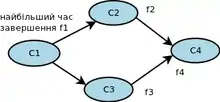
Наслідок: найбільше значення f матиме в компоненті-джерелі (англ. source SCC), тобто вершина лежатиме на верхівці стеку.

f_{1}>f_{2}>f_{4},f_{1}>f_{3}>f_{4}

Складність

Якщо на вході граф описаний за допомогою списком суміжності, алгоритм виконує два повних обходи графу, отже виконується за Θ(V+E) (лінійний) час, який є оптимальним, бо збігається з нижньою межею (кожен алгоритм повинен обійти всі вершини і ребра). Це концептуально найпростіший ефективний алгоритм, але не настільки швидкий як алгоритм Тарджана і алгоритм компонент сильної зв'язності по шляхах, які виконують лише один обхід графу.

Якщо граф представлено через матрицю суміжності, алгоритм потребує час Ο(V²).

Посилання

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.