Алгоритм Тар'яна

Алгоритм Тар'яна — алгоритм пошуку компонент сильної зв'язності в орієнтованому графі, що працює за лінійний час.

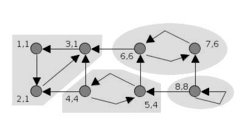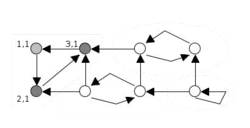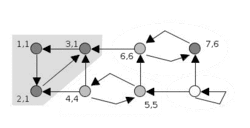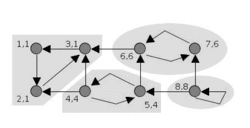анімація алгоритму Тар'яна
Структура даних Граф
Найгірша швидкодія

Цей алгоритм ґрунтується на тому, що:

  1. Вершини розглядаються у зворотному топологічному порядку, тому в кінці рекурсивної функції для початкової вершини не зустрінеться жодна вершина з тієї ж сильної компоненти, оскільки всі вершини, досяжні з початкової, вже опрацьовано.
  2. Зворотні зв'язки в дереві дають інший шлях з однієї вершини в іншу і зв'язують сильні компоненти.

Неформальний опис алгоритму

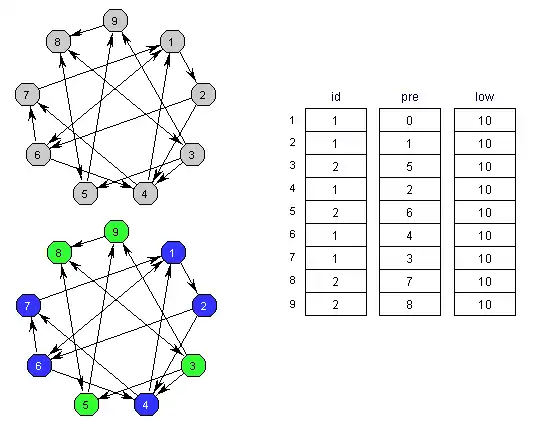
Алгоритм Тар'яна можна розуміти як варіацію алгоритму пошуку в глибину, в якому під час відвідування вершини і при закінченні опрацювання вершини виконуються додаткові дії. Відвідування вершини відбувається при русі від кореня до листя, а закінчення обробки вершини — на зворотному шляху. Під час відвідування вершини вона проштовхується в допоміжний стек, а виштовхується звідти при закінченні опрацювання[1].

Індекси компонент зв'язності всіх вершин зберігаються у векторі id, індексованому номерами вершин. Вектор low відстежує вершину з найменшим номером у прямому порядку обходу, досяжну з кожного вузла через послідовність прямих зв'язків, за якими слідує один висхідний зв'язок. Скориставшись пошуком у глибину з тим, щоб розглядати вершини в зворотному топологічному порядку, для кожної вершини v обчислюється максимальна точка, досяжна через зворотний зв'язок із попередника (low[v]). Коли для вершини v виконується pre[v]=low[v], вона виштовхується зі стека, а також всі вершини вище від неї і всім їм присвоюється номер компоненти[джерело?].

Час роботи

Алгоритм має часову складність , де  — кількість ребер, а  — кількість вершин графу[1].

Див. також

Алгоритм знаходження компонент сильної зв'язності — аналогічний алгоритм, що використовує пошук у глибину.

Примітки
  1. Джереми Сик и др., 2006.


Література
  • Tarjan R. E. Depth-first search and linear graph algorithms // SIAM Journal on Computing. — 1972. — Vol. 1, no. 2 (21 January). — P. 146–160. — DOI:10.1137/0201010.
  • Роберт Седжвик. Алгоритмы на графах = Graph algorithms. — 3-е изд. — Россия, Санкт-Петербург : «ДиаСофтЮП», 2002. — С. 496. — ISBN 5-93772-054-7.
  • Джереми Сик, Лай-Кван Ли, Эндрю Ламсдэйн. C++ Boost Graph Library. — Питер, 2006. — С. 202-205. — ISBN 5-469-00352-3.

Посилання
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.