Вентиль Тоффолі

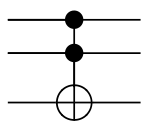
Вентиль Тоффолі (також вентиль CCNOT) — у логічних схемах вентиль, винайдений Томмазо Тоффолі, є універсальним оборотним логічним вентилем, що означає, що будь-яка оборотна схема може бути побудована з вентилів Тоффолі. Він також відомий як вентиль «контрольоване-контрольоване-НЕ», який описує його дію. Він має 3-бітові входи та виходи; якщо перші два біти встановлені в 1, він інвертує третій біт, інакше всі біти залишаються однаковими.

Позначення вентиля Тоффолі на схемі

Основи

Логічний вентиль L є оборотним, якщо для будь-якого виходу y існує унікальний вхід x, такий що виконується L(x) = y. Якщо вентиль L є оборотним, існує зворотний вентиль L′, який відображає y в x, де L′(y) = x. Із загальноприйнятих логічних входів вентиль «НЕ» є оборотним, як це видно з таблиці істинності нижче.

ВХІДВИХІД
01
10

Однак у загальному випадку вентиль «І» не є оборотним. Входи 00, 01 і 10 відображаються на виході в 0.

Оборотні вентилі вивчали з 1960-х років. Початковою мотивацією було те, що оборотні вентилі розсіюють менше тепла (або, в принципі, не розсіюють тепла).[1] Якщо розглянути логічний вентиль як щось, що споживає подане на вхід, інформація втрачається, оскільки на виході наявно менше інформації, ніж на вході. Через цю втрату інформації втрачається енергія до навколишнього середовища у вигляді тепла через термодинамічну ентропію.[2] Іншим способом зрозуміти це є те, що заряди в ланцюзі стікають на землю забираючи з собою невелику кількість енергії, коли вони змінюють стан. Оборотний вентиль лише переміщує стани, і оскільки інформація не втрачається, енергія зберігається.

Більш недавня мотивація походить від квантових обчислень. Квантова механіка вимагає, щоб перетворення були оборотними і дозволяє більш загальні обчислення, ніж класичні комп'ютери (принцип суперпозиції).

Універсальність і вентиль Тоффолі

Будь-який оборотний вентиль, який споживає свої вхідні дані та дозволяє всі вхідні обчислення, повинен мати не більше вхідних бітів, ніж вихідні біти, за принципом Діріхле. Для одного вхідного біта існує два можливих оборотних вентиля. Один з них НЕ. Інший — вентиль ідентичності, який відображає свої вхідні дані у вихідні дані без змін. Для двох вхідних бітів єдиним нетривіальним вентилем є вентиль «контрольоване-НЕ», який виконує операцію «Виключне АБО» першого біта і другого біта і залишає перший біт незмінним.

Таблиця істинностіФорма матриці перестановки
INPUT OUTPUT
 0  0  0  0 
0101
1011
1110

На жаль, є оборотні функції, які неможливо обчислити, використовуючи лише ці вентилі. Іншими словами, набір, що складається з вентилів NOT і XOR, не є універсальним. Щоб обчислити довільну функцію за допомогою оборотних вентилів, нам потрібен інший вентиль. Одним з можливих є вентиль Тоффолі, запропонований Тоффолі в 1980 році.[3]

Цей шлюз має 3-бітові вхід та вихід. Якщо встановлено перші два біти, він змінює на протилежне значення третій біт. Далі наведена таблиця вхідних і вихідних бітів:

Таблиця істинностіФорма матриці перестановки
INPUT OUTPUT
 0  0  0  0  0  0 
001001
010010
011011
100100
101101
110111
111110

Це також можна описати як відображення бітів {a, b, c} в {a, b, c XOR (a AND b)}.

Вентиль Тоффолі універсальний; це означає, що для будь-якої булевої функції f(x1, x2, …, xm), існує ланцюг, що складається з вентилів Тоффолі, який приймає x1, x2, …, xm та деякі додаткові біти, які мають значення 0 або 1 для виходів x1, x2, …, xm, f(x1, x2, …, xm), а також додаткові біти (що називаються сміттєвими). По суті, це означає, що можна використовувати вентиль Тоффолі для побудови систем, які оборотно виконуватимуть обчислення будь-якої бажаної булевої функції.

Пов'язані логічні вентилі
Вентиль Тоффолі може бути сконструйований з одиничних кубітних вентилів і мінімум шести вентилів CNOT.
  • Вентиль Фредкіна — це універсальний оборотний 3-бітовий вентиль, який міняє місцями два останні біти, якщо перший біт дорівнює 1; реалізує операцію керованого обміну.
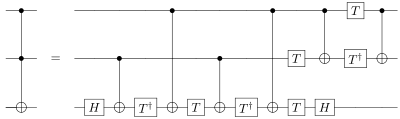
  • n — бітовий вентиль Тоффолі є узагальненням вентиля Тоффолі. Це приймає n біт x1, x2, …, xn у якості входів і віддає n бітів. Перші n−1 вихідних бітів це просто x1, …, xn−1. Останній вихідний біт (x1 AND … AND xn−1) XOR xn . Вентиль Тоффолі може бути реалізовано з п'яти двохкубітних квантових вентилів.[4]Насправді для реалізації вентиля Тоффолі потрібно мінімум п'ять двохкубітних квантових вентилів.[5]
  • Пов'язаний з ними квантовий вентиль Дойча може бути реалізований за допомогою п'яти оптичних імпульсів з нейтральними атомами.[6] Вентиль Дойча — це універсальний вентиль для квантових обчислень.[7]

Відношення до квантових обчислень

Будь-які оборотні вентилі можуть бути реалізовані на квантовому комп'ютері, отже, вентиль Тоффолі також є квантовим оператором. Однак вентиль Тоффолі не може бути використаний для універсальних квантових обчислень, хоча це означає, що квантовий комп'ютер може реалізувати всі можливі класичні обчислення. Вентиль Тоффолі повинен бути реалізований разом з деякими по суті квантовими вентилями, щоб бути універсальним для квантових обчислень. Насправді достатньо будь-якого одиночного кубіта з реальними коефіцієнтами, який може створити нетривіальний квантовий стан.[8] Вентиль Тоффолі на основі квантової механіки був успішно реалізований в січні 2009 року в Університеті Інсбрука, Австрія.[9] Хоча реалізація n-кубітового Тоффолі вимагає 2n CNOT вентилів,[10] застосування взаємодії багатьох тіл може безпосередньої використовувати для роботи вентиль на атомах Ридберга та реалізації надпровідних ланцюгів.[11][12][13]

Примітки
  1. Landauer, R. (July 1961). Irreversibility and Heat Generation in the Computing Process. IBM Journal of Research and Development 5 (3): 183–191. ISSN 0018-8646. doi:10.1147/rd.53.0183.
  2. Landauer, R. (July 1961). Irreversibility and Heat Generation in the Computing Process. IBM Journal of Research and Development 5 (3): 183–191. doi:10.1147/rd.53.0183.
  3. Technical Report MIT/LCS/TM-151 (1980) and an adapted and condensed version: Toffoli, Tommaso (1980). У J. W. de Bakker and J. van Leeuwen. Reversible computing Automata, Languages and Programming, Seventh Colloquium. Noordwijkerhout, Netherlands: Springer Verlag. с. 632–644. ISBN 3-540-10003-2. doi:10.1007/3-540-10003-2_104. Архів оригіналу за 15 квітня 2010.
  4. Barenco, Adriano; Bennett, Charles H.; Cleve, Richard; DiVincenzo, David P.; Margolus, Norman; Shor, Peter; Sleator, Tycho; Smolin, John A. та ін. (Nov 1995). Elementary gates for quantum computation. Physical Review A (American Physical Society) 52 (5): 3457–3467. Bibcode:1995PhRvA..52.3457B. PMID 9912645. arXiv:quant-ph/9503016. doi:10.1103/PhysRevA.52.3457. Проігноровано невідомий параметр |s2cid= (довідка);
  5. Yu, Nengkun; Duan, Runyao; Ying, Mingsheng (30 липня 2013). Five two-qubit gates are necessary for implementing the Toffoli gate. Physical Review A 88 (1): 010304. Bibcode:2013PhRvA..88a0304Y. ISSN 1050-2947. arXiv:1301.3372. doi:10.1103/physreva.88.010304. Проігноровано невідомий параметр |s2cid= (довідка)
  6. Shi, Xiao-Feng (May 2018). Deutsch, Toffoli, and CNOT Gates via Rydberg Blockade of Neutral Atoms. Physical Review Applied 9 (5): 051001. Bibcode:2018PhRvP...9e1001S. arXiv:1710.01859. doi:10.1103/PhysRevApplied.9.051001. Проігноровано невідомий параметр |s2cid= (довідка)
  7. Deutsch, D. (1989). Quantum Computational Networks. Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences 425 (1868): 73–90. Bibcode:1989RSPSA.425...73D. ISSN 0080-4630. JSTOR 2398494. doi:10.1098/rspa.1989.0099. Проігноровано невідомий параметр |s2cid= (довідка)
  8. Shi, Yaoyun (Jan 2003). Both Toffoli and Controlled-NOT need little help to do universal quantum computation. Quantum Information & Computation 3 (1): 84–92. Bibcode:2002quant.ph..5115S. arXiv:quant-ph/0205115.
  9. Monz, T.; Kim, K.; Hänsel, W.; Riebe, M.; Villar, A. S.; Schindler, P.; Chwalla, M.; Hennrich, M. та ін. (Jan 2009). Realization of the Quantum Toffoli Gate with Trapped Ions. Physical Review Letters (American Physical Society) 102 (4): 040501. Bibcode:2009PhRvL.102d0501M. PMID 19257408. arXiv:0804.0082. doi:10.1103/PhysRevLett.102.040501. Проігноровано невідомий параметр |s2cid= (довідка);
  10. Shende, Vivek V.; Markov, Igor L. (2008-03-15). «On the CNOT-cost of TOFFOLI gates». arXiv:0803.2316 [quant-ph].
  11. Khazali, Mohammadsadegh; Mølmer, Klaus (11 червня 2020). Fast Multiqubit Gates by Adiabatic Evolution in Interacting Excited-State Manifolds of Rydberg Atoms and Superconducting Circuits. Physical Review X (англ.) 10 (2): 021054. Bibcode:2020PhRvX..10b1054K. ISSN 2160-3308. doi:10.1103/PhysRevX.10.021054. Проігноровано невідомий параметр |doi-access= (довідка)
  12. Isenhower, L.; Saffman, M.; Mølmer, K. (4 вересня 2011). Multibit CkNOT quantum gates via Rydberg blockade. Quantum Information Processing (англ.) 10 (6): 755. ISSN 1573-1332. arXiv:1104.3916. doi:10.1007/s11128-011-0292-4. Проігноровано невідомий параметр |s2cid= (довідка)
  13. Rasmussen, S. E.; Groenland, K.; Gerritsma, R.; Schoutens, K.; Zinner, N. T. (7 лютого 2020). Single-step implementation of high-fidelity n -bit Toffoli gates. Physical Review A 101 (2): 022308. Bibcode:2020PhRvA.101b2308R. ISSN 2469-9926. arXiv:1910.07548. doi:10.1103/physreva.101.022308. Проігноровано невідомий параметр |s2cid= (довідка)
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.