Вібронна спектроскопія

Під дією електромагнітного випромінювання молекула може перейти з енергетичного стану ${\displaystyle E'}$ до енергетичного стану ${\displaystyle E''}$. Інтенсивність електричного дипольного моменту між цими станами пропорційна квадрату модуля моменту переходу:

${\displaystyle \sum _{A=x,y,z}|\langle {\mathfrak {F}}'|\mu _{A}(\xi ,\theta )|{\mathfrak {F}}''|^{2}}$,

де ${\displaystyle {\mathfrak {F}}',\,\,{\mathfrak {F}}''}$ - власні функції гамільтоніану молекули, які відповідають власним значенням ${\displaystyle E',\,\,E'',\,\,\,\mu _{A}}$ - компонента (${\displaystyle x,y}$ або ${\displaystyle z}$) оператора дипольного моменту молекули, яка залежить від електронних ${\displaystyle \xi }$ та коливальних ${\displaystyle \theta }$ координат. Відповідно до теореми Вігнера-Еккарта, інтеграл ${\displaystyle \langle {\mathfrak {F}}'|\mu _{A}(\xi ,\theta )|{\mathfrak {F}}''\rangle }$ є відмінним від нуля, якщо прямий добуток незвідних представлень ${\displaystyle \Pi ({\mathfrak {F}}')\otimes \Pi ({\mathfrak {F}}'')\otimes \Pi (\mu _{A})}$ містить повносиметричне незвідне представлення. Якщо виключити переміщення у просторі й обертання молекули як цілого, функції ${\displaystyle {\mathfrak {F}}}$ є функціями електронних й коливальних координат. У наближенні Борна-Опенгеймера вони можуть бути преставлені у вигляді добутків:

${\displaystyle {\mathfrak {F}}={\mathfrak {F}}_{oscillatory}(\xi )\cdot {\mathfrak {F}}_{electronic}(\theta ).}$

У цьому випадку квадрат модулю дипольного моменту переходу перетворюється на

${\displaystyle \sum _{A=x,y,z}|\langle {\mathfrak {F}}'_{oscillatory}(\xi )\cdot {\mathfrak {F}}'_{electronic}(\theta )|\mu _{A}(\xi ,\theta )|{\mathfrak {F}}_{oscillatory}''(\xi )\cdot {\mathfrak {F}}_{electronic}''(\theta )\rangle |^{2},}$

а умова того, що інтеграл не прийме значення 0, зводиться до того, що прямий добуток

${\displaystyle \Pi ({\mathfrak {F}}_{oscillatory}')\otimes \Pi ({\mathfrak {F}}_{electronic}')\otimes \Pi ({\mathfrak {F}}_{oscillatory}'')\otimes \Pi ({\mathfrak {F}}_{electronic}'')\otimes \Pi (\mu _{A})}$

повинен містити повносиметричне представлення групи молекули. Це співвідношення називається правилом відбору посиметрії для вібронних (електронно-коливальних) переходів.

Електронні переходи зазвичай спостерігають у видимому та ультрафіолетовому діапазонах, з довжиною хвилі приблизно 200–700 нм (50 000–14 000 см⁻¹), тоді як основні коливання спостерігають нижче приблизно 4000 см⁻¹[4]. Коли електронні та коливальні переходи мають настільки різну зміну енергії, вібронним зв'язуванням (змішуванням електронних та коливальних хвильових функцій) можна знехтувати, і рівні енергії можна вважати сумою електронних та коливальних енергії; тобто справедливе наближення Борна-Оппенгеймера[5]. Повна енергія молеули залежить не тільки від електронного стану, а й від коливальних та обертових квантових чисел, які для двоатомної молекули позначають, відповідно v та J. Заведено додавати подвійний штрих (v${\displaystyle ^{\prime \prime }}$, J${\displaystyle ^{\prime \prime }}$) для основного електонного стану та одинарний штрих (v${\displaystyle ^{\prime }}$, J${\displaystyle ^{\prime }}$) для збудженого електронного стану.

Кожен електронний перехід може мати коливальну структуру, а для молекул у газовій фазі можлива ще й тонка обертальна структура. Це залишається справедливим навіть тоді, коли молекули мають нульовний дипольний момент, тож не мають ні коливально-обертового спектру в інфрачервоному діапазоні, ні чисто обертового спектру в мікрохвильовому діапазоні[6].

Необхідно розрізняти спектри поглинання та випромінювання. При поглинанні молекула починає в основному електронному стані й, зазвичай, в основному коливальному стані ${\displaystyle v''=0}$ теж, бо при звичних температурах енергія, необхідна для збудження коливання велика в порівнянні з тепловою. Молекула збуджуєть в інший електронний стан і може опинитися в одному з багатьох коливальних станах ${\displaystyle v'=0,1,2,3,...}$. При випромінюванні початковий стан молекули може бути одним із багатьох коливальних станів, а кінцевим станом буде основний електронний стан і один із багатьох коливальних станів. Спектр випромінювання молекули набагато складніший, ніж спектр поглинання, оскільки є набагато більше можливостей зміни енергії коливань.

Потенціал Морзе (блакитний) та гармонічний потенціал (зелений). На скінченній міжмолекулярній відстані потенціал визначає енергію дисоціації чисто коливального спектру. Для вібронних спектрів є дві потенціальні криві (рисунок праворуч), і межа дисоціації є енергією верхнього стану на нескінченній відстані.

Діаграма рівнів енергії, що ілюструє принцип Франка — Кондона. Переходи між ${\displaystyle v''=0}$ та ${\displaystyle v'=2}$ мають найбільшу імовірність.

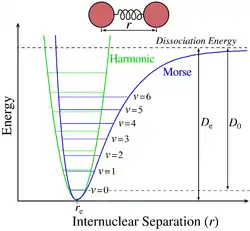
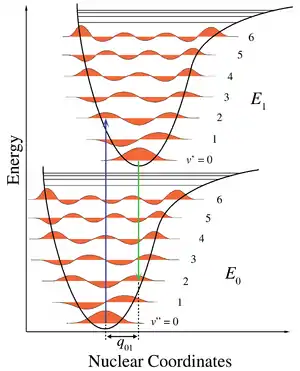
У спектрах поглинання коливальна структура для заданого електронного переходу утворює просту прогресію, або серію переходів зі спільним рівнем, тут найнижчим рівнем з ${\displaystyle v''=0}$[7]. Для коливальних квантових чисел нема жодних правил відбору. В основному стані молекула має нульове коливальне квантове число, але в збудженому електронному стані коливальне квантове число може бути довільним. Величини термів ${\displaystyle G(v)}$ для гармонічного осцилятора задаються формулою

${\displaystyle G(v)={\bar {\nu }}_{electronic}+\omega _{e}(v+{1 \over 2})\,}$

де v позначає коливальне квантове число, ω_e є власною частотою осцилятора. У наступному наближенні терми стають

${\displaystyle G(v)={\bar {\nu }}_{electronic}+\omega _{e}(v+{1 \over 2})-\omega _{e}\chi _{e}(v+{1 \over 2})^{2}\,}$

де χ_e позначає сталу ангармонічності. Це краще наближення потенціалу Морзе поблизу мінімуму. Проміжок між сусідніми коливальними лініями зменшується зі збільшенням коливального квантового числа через ангармонічність коливань. Врешті-решт цей проміжок стає нульовим там, де молекула дисоціює в неперервний спектр. Друга з наведених формул адекватно описує діапазон малих коливальних квантових чисел. Для більших значень, там де молекула наближається до межі дисоціації, потрібно враховувати нові ангармонічні члени. Енергія дисоціації відповідає верхньому (граничному) стану потенціальної кривої на нескінченній відстані між ядрами атомів.

Інтенсивності дозволених вібронних переходів підкоряються принципу Франка-Кондона[8]. Оскільки електронні переходи дуже швидкі порівняно зі зміщеннями атомних остовів, коливальні переходи відбуваються частіше, коли вони відповідають найменшій зміні координат атомів, тобто тоді, коли переходи вертикальні на діаграмі рівнів енергії. Кожна лінія має скінченну ширину, що залежить від різноманітних чинників[9].

Вібронні спектри двоатомних молекул в газовій фазі добре вивчено[10]. Вібраційна структура іноді спостерігається в рідині та твердотільній фазі, а також у розчині. Споріднені явища, зокрема спектроскопія фотоелектронів, резонансна раман-спектроскопія, люмінесценція та флуорисценція, в цій статті не розглядаються, хоча там теж відбуваються вібронні переходи.

Вібронні спектри двоатомних молекул у газі мають також обертальну структуру. Кожна лінія в коливальній серії має P- та R-гілки. Для деяких електронних переходів спостерігається також Q-гілка. Енергії переходів, в обернених сантиметрах, для ліній певного вібронного переходу наведено в наближенні жорсткого ротатора, тобто нехтуючи відцентровими спотвореннями, в книзі[11]

${\displaystyle G(J^{\prime },J^{\prime \prime })={\bar {\nu }}_{v^{\prime }-v^{\prime \prime }}+B^{\prime }J^{\prime }(J^{\prime }+1)-B^{\prime \prime }J^{\prime \prime }(J^{\prime \prime }+1).}$

Тут B позначає обертальну сталу, а J обертальне квантове число. (Для B подвійний штрих вказує основний стан, а одинарний - електронний збуджений стан). Значення обертальних сталих можуть значно відрізнятися, оскільки довжина зв'язку в збудженому електронному стані може бути зовсім іншою від довжини зв'язку в основному стані. Тут діє принцип Франка-Кондона. Обертальна стала пропорційна довжині зв'язку. Зазвичай B′ < B′′, бо відстань між атомними остовами як правило зростає, коли електронний стан молекули змінюється від зв'язаної орбіталі до антизв'язаної орбіталі. Але це не завжди так; якщо електрон переходить із незв'язаної орбіталі в зв'язану, довжина зв'язку може зменшитися, і тоді B′ > B′′.

Діаграма Фортрата для B′=0.8, B′′=1, на якій видно зміщення обертальних ліній від коливального рівня (при 0 см⁻¹). Відцентрове спотворення на цій діаграмі не враховано.

Розгляд обертової тонкої структури вібронних переходів аналогічний тому, як це робиться для ротаційно-вібраційної спектроскопії. Принципова візниця в тому, що основний та збуджений стани є різними електронними станами, аналогічно для коливальних рівнів. Для P-гілки ${\displaystyle J^{\prime }=J^{\prime \prime }-1}$, тому

${\displaystyle {\bar {\nu }}_{P}={\bar {\nu }}_{v'-v''}+B'(J''-1)J''-B''J''(J''+1)}$

${\displaystyle ={\bar {\nu }}_{v'-v''}-(B'+B'')J''+(B'-B''){J''}^{2}.}$

Для R-гілки ${\displaystyle J''=J'-1}$, що означає

${\displaystyle {\bar {\nu }}_{R}={\bar {\nu }}_{v'-v''}+B'J'(J'+1)-B''J'(J'-1)}$

${\displaystyle ={\bar {\nu }}_{v'-v''}+(B'+B'')J'+(B'-B''){J'}^{2}.}$

Частоти переходів у P- та R- гілках об'єднує, в першому наближенні, формула[11][12]

${\displaystyle {\bar {\nu }}_{P,R}={\bar {\nu }}_{v^{\prime },v^{\prime \prime }}+(B^{\prime }+B^{\prime \prime })m+(B^{\prime }-B^{\prime \prime })m^{2},\quad m=\pm 1,\pm 2\ldots }$

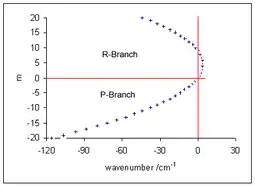
Тут додатні значення m відповідають R-гілці (коли m = +J), а від'ємні - P-гілці (m = -J). Частоти ліній P-гілки, нижче від нульового рівня смуги при ${\displaystyle {\bar {\nu }}_{v^{\prime },v^{\prime \prime }}}$, зростають з m. У R-гілці, для звичного випадку B′ < B′′, зі зростанням J частоти спочатку зростають вище від нульового рівня смуги, але потім спадають і врешті-решт опиняються на нижньому боці. Цей ефект демонструє діаграма Фортрата[13]. У наближенні жорсткого ротатора частоти вкладаються на параболу з максимумом при

${\displaystyle x=-{\frac {B^{\prime }+B^{\prime \prime }}{2(B^{\prime }-B^{\prime \prime })}}.}$

лінія R-гілки з найвищою частотою відома також під назвою голова смуги. Вона відповідає значенню m, до дорівнює цілій частині of x або (x+1).

Коли Q-гілка для певного електронного переходу дозволена, її лінії відповідають ситуації ∆J=0, J′=J′′, і частоти задаються формулою[14]

${\displaystyle {\bar {\nu }}_{Q}={\bar {\nu }}_{v',v''}+(B'-B'')J(J+1)\quad J=1,2\ldots }$

Тоді Q-гілка є серією ліній зі зростанням проміжку між лініями з ростом J. Коли B′<B′′, Q-гілка лежить нижче нульової лінії коливального переходу.

Застосування

Спектр блакитного полум'я бутанового факела, на якому видно смугу випромінювання молекулярного радикалу та смуги Свона, що виникають завдяки утворенню C₂.

Аналіз вібронних спектрів двоатомних молекуль дає інформацію як про основний електронний стан, так і про збуджений електронний стан. Дані про основний стан можна здобути методами вібраційної або чисто ротаційної спектроскопії, але дані про збуджений стан можна отримати тільки з аналізу вібронних спектрів. Наприклад, довжину зв'язку в збудженому стані можна визначити зі значення сталої обертання B′.

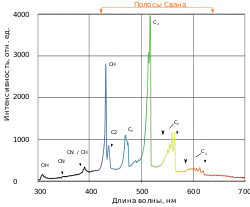
Крім вивчення стабільних двоатомних молекул вібронна спектроскопія використовується для дослідження нестабільних хімічних утворень, зокрема CH, NH, радикалу гідроксилу, OH, та радикалу ціану CN[16]. Смуги Свона в спектрах полум'я вуглеводню є серією коливань зв'язку C-C радикалу дикарбону C₂ для електронного переходу ${\displaystyle d^{3}\Pi _{u}\Leftrightarrow a^{3}\Pi _{g}}$[17]. Вібронні смуги спостерігалися в інфрачервоному та ультрафіолетовому діапазонах для 9 інших електронних переходів C₂.[2].

Формальдигід

Для багатоатомних молекул серії часто спостерігаються, коли зміни довжини зв'язку при електромагнінтому збудженні збігаються зі змінами, що притаманні ″повністю симетричним″ коливанням[18]. Процес аналогічний тому, що відбувається в резонансній раман-спектроскопії. Наприклад у метаналі (формальдегіді), H₂CO, n → π* перехід означає збудження електрона з байдужої до утворення зв'язків орбіталі на антизв'язану пі-орбіталь, що ослабляє і видовжує C-O зв'язок. Це дає довгу серію коливань з розтягом C-O зв'язку[19][20]. Молекула бензолу C₆H₆ дає ще один приклад. Як у газовій, так і рідкій фазі, смуга 250 нм має серію, що відповідає симетричним дихальним коливанням[21].

Спектр поглинання водного розчину перманганату калію.

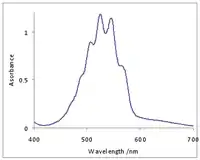
Приклад із неорганічної хімії: іон перманганату Mn₄^- у водному розчині має інтенсивний фіолетовий колір завдяки смузі з переносом заряду ліганд-метал O → Mn, яка займає більшу частину видимого діапазону[22]. Ця смуга має структуру завдяки коливанням з розтягом зв'язку Mn-O [23]. Індивідуальні лінії прекриваються, утворюється широка полоса із деякою структурою.

Можуть спостерігатися серії, що відповідають не повністю симетричним коливанням[24].

d-d переходи в атомах, що розміщенні в центральносиметричній позиції, заборонені в дипольному наближенні правилом Лапорта. Це стосується октраедничних координаційних сполук перехідних металів. Спектри багатьох таких комплексів мають почасти вібронний характер[25]. Те ж правило стосується f-f переходів у центросиметричних комплексах лантаноїдів та актинідів. У випадку октаедричного актинідногго хлор-комплексу урану(IV) UCl₆²⁻, електронний спектр повністю вібронний. При температурі рідкого гелію, 4K, окремі лінії в спектрі вдалося повністю розділити, чисто електронний перехід має нульову інтенсивність, а три сателіти відповідають асиметричним коливанням зв'язку U-Cl, дві - асиметричним модам зі згинанням Cl-U-Cl[26]. Пізніші дослідження того ж аніона змогли також пояснити вібронний перехід з низькочастотними коливаннями ґратки[27].

• Atkins, P. W.; de Paula, J. (2006). Physical Chemistry (вид. 8th). Oxford University Press. с. 431–469. ISBN 0198700725. Chapter: Molecular Spectroscopy 2.
• Banwell, Colin N.; McCash, Elaine M. (1994). Fundamentals of molecular spectroscopy (вид. 4th). McGraw-Hill. ISBN 0-07-707976-0.
• Gaydon, Alfred Gordon (1974). The spectroscopy of flames. London: Chapman and Hall. ISBN 0-470-29433-7.
• Hollas, M. J. (1996). Modern Spectroscopy (вид. 3rd). Wiley. ISBN 0471965227.
• Straughan, B. P.; Walker, S. (1976). Spectroscopy 3 (вид. 3rd). Chapman and Hall. с. 50–84. ISBN 0-412-13390-3.