Граф Ламана

Графи Ламана виникають в теорії жорсткості наступним чином: якщо розмістити вершини графу Ламана на евклідовій площині так, щоб вони перебували у загальному положенні, і рухати вершини так, щоб довжини всіх ребер залишалися незмінними, то цей рух з необхідністю буде евклідовою ізометрією. Більш того, будь-який мінімальний граф, що має таку властивість, з необхідністю є графом Ламана. З інтуїтивної точки зору зрозуміло, що кожне ребро графу зменшує ступінь вільності відповідної йому шарнірно-стрижневої системи на одиницю. Тому 2n-3 ребер в графі Ламана зменшують 2n ступенів вільності системи з n вершин до трьох, що відповідає ізометричному перетворенню площини. Граф є жорстким в цьому сенсі тоді і лише тоді, коли він містить підграф Ламана, що містить всі вершини графу. Таким чином, графи Ламана є мінімальними жорсткими графами, і вони формують базис двомірних матроїдів жорсткості.

Якщо задані n точок площини, існує 2n ступенів вільності в їх розташуванні (кожна точка має дві незалежні координати), але жорсткий граф має лише три ступені вільності (розміщення однієї точки та поворот навколо цієї точки). Інтуїтивно зрозуміло, що додавання ребра фіксованої довжини в граф скорочує ступінь вільності на одиницю, так що 2n-3 ребер графу Ламана зменшує 2n ступенів вільності початкового розташування до трьох ступенів вільності жорсткого графу. Проте не кожен граф з 2n-3 ребрами є жорстким. Умова у визначенні графу Ламана, що жоден підграф не містить забагато ребер гарантує, що кожне ребро реально вносить свій внесок у загальне зменшення ступеня вільності, а не є частиною підграфу, який вже є жорстким завдяки іншим своїм ребрам.

Графи Ламана пов'язані також з поняттям псевдотріангуляції. Відомо, що кожна псевдотріангуляція є графом Ламана, і навпаки, кожен плаский граф Ламана може бути реалізований як псевдотріангуляція.[2] Проте слід мати на увазі, що існують непланарні графи Ламана, наприклад, повний дводольний граф ${\displaystyle K_{3,3}}$.

Штрейну та Теран[3] визначають граф як ${\displaystyle (k,l)}$-розріджений, якщо будь-який непорожній підграф з ${\displaystyle n}$ вершинами має максимум ${\displaystyle kn-l}$ ребер, і ${\displaystyle (k,l)}$-щільний, якщо він ${\displaystyle (k,l)}$-розріджений і має в точності ${\displaystyle kn-l}$ ребер. Таким чином, у цій нотації, графи Ламана — це в точності (2,3)-щільні графи, і підграфи графів Ламана — це в точності (2,3)-розріджені графи. Ту ж саму нотацію можна використовувати для опису інших важливих сімейств розріджених графів, включаючи дерева, псевдоліси, і графи з обмеженою древесністю[4].

Побудова Хенненберга веретена Мозера

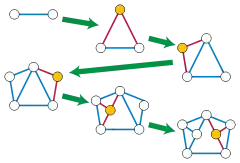
Задовго до роботи Ламана Лебрехт Хеннеберг описав двомірні мінімальні жорсткі графи (тобто, графи Ламана) різними способами.[5] Хенненберг показав, що мінімальні жорсткі графи з двома та більше вершинами — це в точності графи, які можна отримати, почавши з одиничного ребра, використовуючи операції двох видів:

1. Додається нова вершина разом з ребрами, що з'єднують її з двома вже наявними вершинами.
2. Ребро розбивається і додається нове ребро, що з'єднує знову з'явилася вершину з наявною.

Послідовність таких операцій, яка формує заданий граф, називається побудовою Хенненберга. Наприклад, повний дводольний граф ${\displaystyle K_{3,3}}$ може бути побудований спочатку застосуванням тричі першої операції для побудови трикутників, а потім застосуванням двох операцій типу два для розбиття двох сторін трикутника.