Доповнення графа
В теорії графів, доповнення або обернений до графу G — граф H на тих самих вершинах, поєднаних ребрами тоді і тільки тоді, коли вони несуміжні в G. Тобто, для побудови доповнення графу, потрібно додати всі ребра, необхідні для отримання повного графу і видалити всі ребра, які були присутні до того. Однак, це не доповнення множини графу; доповнені тільки ребра.
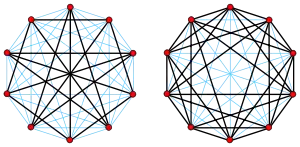
Граф Петерсена (ліворуч) і його доповнення (праворуч)
Формальна побудова
Нехай G = (V, E) буде простим графом і нехай K складається з усіх 2-елементних підмножин V. Тоді H = (V, K \ E) — доповнення G.
Застосування і приклади
Декілька концепцій теорії графів стосуються одна одної через доповнення графів:
- Доповнення безреберного графу це повний граф і навпаки.
- Незалежна множина в графі це кліка в доповненні графу і навпаки.
- Доповнення будь-якого графу без трикутників це граф без кігтів.
- Самодоповняльний граф це граф, який ізоморфний до свого доповнення.
- Кографи визначені як графи, які можна утворити з диз'юнктного об'єднання і операцій доповнення, і які формують сім'ю самодоповнювальних графів: доповнення будь-якого кографу є інший (можливо інший) кограф.
Посилання
- Bondy, John Adrian; Murty, U. S. R. (1976). Graph Theory with Applications. North-Holland. ISBN 0-444-19451-7. Процитовано 30 травня 2013., pages 6 and 29.
- Diestel, Reinhard (2005). Graph Theory (вид. 3rd). Springer. ISBN 3-540-26182-6.. Electronic edition, page 4.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.