Кограф

Будь-який кограф можна побудувати, дотримуючись таких правил:

1. Будь-яка окрема вершина графу є кографом;
2. Якщо ${\displaystyle G}$ — кограф, то його доповнення ${\displaystyle {\overline {G}}}$ теж кограф;
3. Якщо ${\displaystyle G}$ і ${\displaystyle H}$ — кографи, то їх незв'язане об'єднання ${\displaystyle G\cup H}$ теж кограф.

Можна дати кілька інших описів кографів. Серед них:

• Кограф — це граф, що не містить шляху P₄ з 4 вершинами (тобто довжини 3) як породженого підграфу. Таким чином, граф є кографом тоді й лише тоді, коли для будь-яких чотирьох вершин ${\displaystyle v_{1},v_{2},v_{3},v_{4}}$, якщо ${\displaystyle \{v_{1},v_{2}\},\{v_{2},v_{3}\}}$ і ${\displaystyle \{v_{3},v_{4}\}}$ — ребра графу, то хоча б одне з ${\displaystyle \{v_{1},v_{3}\},\{v_{1},v_{4}\}}$ або ${\displaystyle \{v_{2},v_{4}\}}$ теж є ребром[7].
• Кограф — це граф, усі породжені підграфи якого мають властивість, що будь-яка максимальна кліка перетинається з будь-якою максимальною незалежною множиною в єдиній вершині.
• Кограф — це граф, у якому будь-який нетривіальний породжений підграф має принаймні дві вершини з однаковими околами.
• Кограф — це граф, у якому будь-який зв'язний породжений підграф має незв'язне доповнення.
• Кограф — це граф, у всіх зв'язних породжених підграфів якого діаметр не перевищує 2.
• Кограф — це граф, у якому будь-яка компонента зв'язності є дистанційно-успадковуваним графом з діаметром, що не перевищує 2.
• Кограф — це граф, клікова ширина якого не перевершує 2[8].
• Кограф — це граф порівнянності послідовно-паралельного часткового порядку[1].
• Кограф — це граф перестановки розділюваної перестановки[9].

Всі повні графи, повні дводольні графи, порогові графи і графи Турана є кографами. Будь-який кограф є дистанційно-успадковуваним досконалим графом порівнянності.

Кодерева і відповідні кографи. Кожне ребро (u, v) в кографі має відповідний колір найближчого спільного предка вершин u і v в кодереві.

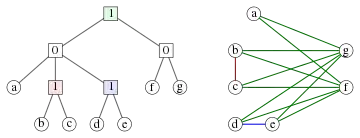
Кодерево — це дерево, в якому внутрішні вершини позначені числами 0 і 1. Будь-яке кодерево T визначає кограф G, який має вершинами листя кодерева T, а дерево, що має корінь у вершині T, відповідає породженому підграфу в G, визначеному множиною листків-нащадків цієї вершини:

• Піддерево, що складається з єдиного листка відповідає породженому підграфу з єдиною вершиною.
• Піддерево, що має коренем вершину з міткою 0 відповідає об'єднанню підграфів, утворених нащадками вершини.
• Піддерево, що має коренем вершину з міткою 1 відповідає з'єднанню підграфів, утворених нащадками вершини. Тобто, формуємо об'єднання і додаємо ребро між будь-якими двома вершинами, що відповідають двом листкам, розташованим у різних піддеревах. Можна також розглядати з'єднання як доповнення всіх графів, утворених об'єднанням доповнень, з подальшою побудовою доповнення отриманого об'єднання.

Еквівалентний шлях побудови кографу з кодерева полягає в тому, що дві вершини з'єднують ребром в тому і тільки в тому випадку, коли найменший спільний предок відповідних листків позначений 1. І навпаки, будь-який кограф можна подати кодеревом таким способом. Якщо зажадати, щоб усі мітки на всіх шляхах від кореня до листя чергувалися, таке подання буде єдиним[7].

Кограф можна розпізнати за лінійний час і побудувати при цьому подання кодерева, якщо використовувати модульне розкладання[10], очищення розкладання[11] або розкладання розщепленням[12]. Як тільки кодерево побудовано, багато знайомих задач теорії графів можна розв'язати за допомогою проходу знизу вгору кодеревом.

Наприклад, щоб знайти максимальну кліку в кографі, обчислюємо, проходячи знизу вгору, максимальну кліку в кожному підграфі, поданому піддеревом кодерева. Для кожної вершини з міткою 0 максимальна кліка — це максимальна кліка, отримана у нащадків вершини. Для вершини з міткою 1 максимальна кліка буде об'єднанням клік, обчислених для нащадків вершини, а розмір цієї кліки дорівнює сумі розмірів клік. Таким чином, поперемінно беручи максимальний розмір і підсумовуючи значення для кожної вершини кодерева, ми обчислимо максимальний розмір кліки, а поперемінно вибираючи максимальну кліку і об'єднуючи, побудуємо саму максимальну кліку. Схожий підхід проходу знизу вгору дозволяє отримати максимальну незалежну множину, хроматичне число, максимальне клікове покриття та існування гамільтонового шляху за лінійний час. Можна також використовувати кодерева для визначення за лінійний час чи є два кографи ізоморфними.

Якщо H — породжений підграф кографу G, то H сам є кографом. Кодерево для H можна отримати видаленням частини листків з кодерева для G з подальшим злиттям вершин, що мають єдиного нащадка. З теореми Крускала про дерева випливає, що відношення «бути породженим підграфом» є хорошим квазіпорядком на кографах[13]. Так, якщо сімейство кографів (таких як планарні кографи) замкнуте відносно операції побудови породженого підграфу, то воно має скінченне число заборонених породжених підграфів. З точки зору обчислень, це означає, що перевірку, чи належить граф до такого сімейства, можна виконати за лінійний час, якщо використовувати прохід знизу вгору кодеревом заданого графу.

• Prosenjit Bose, Jonathan Buss, Anna Lubiw. Pattern matching for permutations // Information Processing Letters. — 1998. — Т. 65 (23 січня). — С. 277—283. — DOI:10.1016/S0020-0190(97)00209-3.
• Andreas Brandstädt, Van Bang Le, Jeremy P. Spinrad. Graph Classes: A Survey. — SIAM Monographs on Discrete Mathematics and Applications, 1999. — ISBN 978-0-89871-432-6.
• M. Burlet, J. P. Uhry. Topics on Perfect Graphs. — 1984. — Т. 21 (23 січня). — С. 253—277.
• D. G. Corneil, H. Lerchs, L. Stewart Burlingham. Complement reducible graphs // Discrete Applied Mathematics. — 1981. — Т. 3, вип. 3 (23 січня). — С. 163—174. — DOI:10.1016/0166-218X(81)90013-5.
• D. G. Corneil, Y. Perl, L. K. Stewart. A linear recognition algorithm for cographs // SIAM Journal on Computing. — 1985. — Т. 14, вип. 4 (23 січня). — С. 926—934. — DOI:10.1137/0214065.
• B. Courcelle, S. Olariu. Upper bounds to the clique width of graphs // Discrete Applied Mathematics. — 2000. — Т. 101, вип. 1—3 (23 січня). — С. 77—144. — DOI:10.1016/S0166-218X(99)00184-5.
• Peter Damaschke. Induced subgraphs and well-quasi-ordering // Journal of Graph Theory. — 1990. — Т. 14, вип. 4 (23 січня). — С. 427—435. — DOI:10.1002/jgt.3190140406.
• Emeric Gioan, Christophe Paul. Split decomposition and graph-labelled trees: characterizations and fully-dynamic [sic] algorithms for totally decomposable graphs. — 2008. — 23 січня.
• Michel Habib, Christophe Paul. A simple linear time algorithm for cograph recognition // Discrete Applied Mathematics. — 2005. — Т. 145, вип. 2 (23 січня). — С. 183—197. — DOI:10.1016/j.dam.2004.01.011.
• H. A. Jung. On a class of posets and the corresponding comparability graphs // Journal of Combinatorial Theory, Series B. — 1978. — Т. 24, вип. 2 (23 січня). — С. 125—133. — DOI:10.1016/0095-8956(78)90013-8.
• H. Lerchs. On cliques and kernels. — Tech. Report, Dept. of Comp. Sci., Univ. of Toronto, 1971. — 23 січня.
• D. Seinsche. On a property of the class of n-colorable graphs // Journal of Combinatorial Theory, Series B. — 1974. — Т. 16, вип. 2 (23 січня). — С. 191—193. — DOI:10.1016/0095-8956(74)90063-X.
• D. P. Sumner. Dacey graphs // J. Austral. Math. Soc.. — 1974. — Т. 18, вип. 04 (23 січня). — С. 492—502. — DOI:10.1017/S1446788700029232.

• cograph graphs. Information System on Graph Class Inclusions.
• Weisstein, Eric W. Cograph(англ.) на сайті Wolfram MathWorld.