Зворотне поширення в часі

ЗПЧ розгортає рекурентну нейронну мережу в часі.

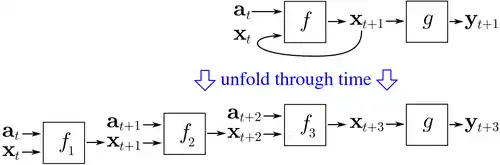
Тренувальні данні для ЗПЧ повинні бути впорядкованою послідовністю пар входів-виходів, ${\displaystyle \langle \mathbf {a} _{0},\mathbf {y} _{0}\rangle ,\langle \mathbf {a} _{1},\mathbf {y} _{1}\rangle ,\langle \mathbf {a} _{2},\mathbf {y} _{2}\rangle ,...,\langle \mathbf {a} _{k-1},\mathbf {y} _{k-1}\rangle }$. Для ${\displaystyle \mathbf {x} _{0}}$ мусить бути вказано початкове значення. Для цієї мети зазвичай застосовують вектор з усіх нулів.

ЗПЧ починається з розгортання рекурентної нейронної мережі в часі, як показано на цьому зображенні. Ця рекурентна нейронна мережа містить дві нейронні мережі прямого поширення, f та g. Коли ця мережа розгортається в часі, то розгорнута мережа містить k примірників f, і один примірник g. У наведеному прикладі мережу було розгорнуто до глибини k = 3.

Потім тренування відбувається подібним чином, як і при тренуванні нейронної мережі прямого поширення зворотним поширенням, за тим виключенням, що тренувальні зразки відвідуються послідовно. Кожен тренувальний зразок складається з ${\displaystyle \langle \mathbf {x} _{t},\mathbf {a} _{t},\mathbf {a} _{t+1},\mathbf {a} _{t+2},...,\mathbf {a} _{t+k-1},\mathbf {y} _{t+k}\rangle }$. (Всі дії для k моментів часу потрібні тому, що розгорнута мережа містить входи на кожному з розгорнутих рівнів.) Після представлення зразка для тренування уточнення ваг у кожному з примірників f (${\displaystyle f_{1},f_{2},...,f_{k}}$) підсумовуються, і потім застосовуються до всіх примірників f. Як початкове значення ${\displaystyle \mathbf {x} }$, як правило, використовують нульовий вектор.

Псевдокод ЗПЧ:

Зворотне_поширення_в_часі(a, y)       // a[t] є входом у момент часу t. y[t] є виходом
    Розгорнути мережу, щоби містила k примірників f
    повторювати до досягнення критерію зупинки:
        x = вектор нульової величини; // x є поточним контекстом
        для t від 0 до n - k          // t є часом. n є довжиною тренувальної послідовності
            Встановити входи мережі в x, a[t], a[t+1], ..., a[t+k-1]
            p = поширити входи в прямому напрямку всією розгорнутою мережею
            e = y[t+k] - p;           // похибка = ціль - передбачення
            Поширити в зворотному напрямку похибку e всією розгорнутою мережею
            Підбити загальну суму змін ваг у k примірниках f.
            Уточнити всі ваги в f та g.
            x = f(x, a[t]);           // обчислити контекст для наступного моменту часу

ЗВЧ має схильність бути значно швидшим для тренування рекурентних нейронних мереж, ніж методики оптимізації загального призначення, такі як еволюційна оптимізація.[4]

ЗВЧ зазнає труднощів з локальними оптимумами. В рекурентних нейронних мережах локальний оптимум є набагато значнішою проблемою, ніж у нейронних мережах прямого поширення.[5] Рекурентний зворотний зв'язок у таких мережах має схильність створювати хаотичні реакції в поверхні похибки, в результаті чого локальні оптимуми виникають часто, і в дуже поганих місцях поверхні похибки.

• Зворотне поширення структурою