Кардинальні точки (оптика)

В Гауссовій оптиці, кардинальні точки це множина із трьох пар точок, що знаходяться на оптичній осі фокусної оптичної системи що має обертову симетрію. Це є фокусні точки, головні точки і вузлові точки.[1] Для ідеальних систем, основні властивості зображення такі як: розмір зображення, орієнтація і положення повністю визначаються розташуванням кардинальних точок; насправді необхідними є лише чотири точки: фокусні точки і головні або вузлові точки. Єдиною ідеальною системою, яка була досягнута на практиці є плоске дзеркало,[2] однак кардинальні точки широко використовуються для апроксимації поведінки реальних оптичних систем. Кардинальні точки дозволяють аналітичного спрощення системи із багатьма компонентами, що дозволяє точно оцінювати властивості зображення системи за допомогою простих розрахунків.

Пояснення
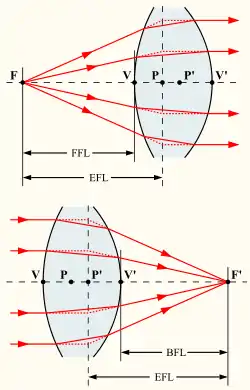
Кардинальні точки товстої лінзи в повітряному середовищі.
F, F' передня і задня фокусні точки,
P, P' передня і задня головні точки,
V, V' передня і задня вершини поверхні.

Кардинальні точки знаходяться на оптичній осі оптичної системи. Кожна точка визначається впливом оптичної системи на промені, які проходять через ту точку, в рамках паралаксіальної апроксимації. Паралаксіальна апроксимація передбачає, що промені проходять під малим кутом по відношенню до оптичної осі, так що і .[3] Ефекти апертури ігноруються: промені які не проходять через апертуру зупиняються за системою і не розглядаються.

Фокусні площини

Передня фокусна точка оптичної системи, за визначенням, має властивість, що кожен промінь, який проходить крізь неї буде проходити через систему паралельно оптичній осі. Задня фокусна точка має зворотню властивість: промені що входять в систему паралельно оптичній осі фокусуються таким чином, що вони проходять через задню фокусну точку.

Промені, які полишають об'єкт із однаковим кутом перетинають задню фокусну площину.

Передня і задня фокусні площини визначаються як такі площини, що є перпендикулярними до оптичної осі, яка проходить через передню і задню фокусні точки. Об'єкт, який знаходиться на нескінченно віддаленій відстані від оптичної системи утворює зображення на задній фокусній площині. Об'єкти на скінченній відстані, формують зображення в іншому місці, але промені, які полишають об'єкт паралельно один до одного перетинаються на задній фокусній площині.

Фільтрування променів під відповідними кутами за допомогою апертури на задній фокусній площині.

Діафрагма або "перегородка" на задній фокусній площині може використовуватися для відфільтровування променів світла за їх кутом, оскільки:

  1. Вона дозволяє проходити променям, які випромінюються під достатньо малим кутом (відносно оптичної осі). (Нескінченно мала апертура дозволить проходити лише тим променям, які випромінюються здовж оптичної осі.)
  2. Не важливо з якої частини об'єкта приходить промінь, промінь буде потрапляти через апертуру, якщо кут з яким він випромінюється від об'єкта достатньо малий.

Важливо, що апертура повинна центруватися відносно оптичної осі аби це працювало як зазначено. Використання достатньо малої апертури в фокусній площині зробить об'єктив телецентричним.

Аналогічно, допустимий діапазон кутів на вихідній стороні об'єктива може фільтруватися розміщенням апертури перед фокусною площиною об'єктиву (або лінзи). Це важливо для цифрових дзеркальних камер, що мають CCD сенсори. Пікселі таких сенсорів більш чутливі до світла, що потрапляє на них прямими променями ніж тими, що потрапляють під кутом. Об'єктив, який не контролює кут падіння променів на детектор буде створювати ефект віньєтування пікселів на зображенні.

Головні площини і точки
Різні форми лінз, і розташування головних площин.

Дві головні площини мають властивість, що промінь, який виходить від лінзи перетинає задню головну площину на тій самій відстані від осі, на якій цей промінь, перетинає передню головну площину, якщо дивитися на лінзу з переду. Це означає що лінзу можна розглядати як головну площину, в якій відбувається заломлення усіх променів. Головні площини мають вирішальне значення для визначення оптичних властивостей системи, оскільки це визначає відстань між об'єктом і зображенням від передньої і задньої головних площин, яке визначає збільшення системи. Головні точки це такі точки в яких головні площини перетинають оптичну вісь.

Якщо середовище, яке оточує оптичну систему має показник заломлення 1 (тобто, повітря або вакуум), тоді відстань від головних точок до відповідних фокусних точок буде дорівнювати лише фокусній довжині системи. В більш загальних випадках, відстань до фокусів дорівнюватиме фокусній відстані помноженій на показник заломлення середовища.

Вузлові точки
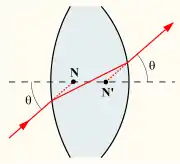
N, N' Передня і задня вузлові точки товстої лінзи.

Передня і задня вузлові точки мають властивість, згідно з якою промінь, що спрямований на одну з них, буде заломлюватися лінзою таким чином так ніби він виходить з іншої, і матиме такий самий кут відносно оптичної осі. Вузлові точки діють відносно кутів так само, як головні точки до відстані перетину. Якщо середовище з обох боків оптичної системи є однаковим (повітря), тоді передня і задня вузлові точки збігаються з передньою і задньою основними точками, відповідно.

Зустрічається, що вузлові точки часто розуміють не вірно в фотографії, де часто стверджують, що промені світла "перетинаються" у "вузлових точках", і що основна діафрагма об'єктиву розташована там, і що це є правильна точка опори для панорамної фотографії, яка дає можливість уникнути помилку паралаксу.[4][5][6] Ці ствердження виникають від плутанини в оптиці об'єктива, а також від плутання різниці між вузловими точками і іншими кардинальними точками системи. (Кращою точкою для вибору осі повороту камери при панорамній фотографії є центр вхідної лінзи системи. [4][5][6] З іншого боку, камери з поворотним об'єктивом із фіксованою позицією плівки повертають об'єктив довкола задньої вузлової точки аби стабілізувати зображення на плівці.[6][7])

Поверхневі вершини

Поверхневі вершини, це точки в який кожна оптична поверхня перетинає оптичну вісь. Вони важливі в першу чергу тому що є параметрами, які можна виміряти фізично для даної позиції оптичних елементів, після чого можна визначити позиції кардинальних точок відносно вершин аби описати фізичну систему.

В анатомії, поверхневі вершини кришталика ока називаються переднім і заднім полюсами кришталика.[8]

Примітки
  1. Greivenkamp, John E. (2004). Field Guide to Geometrical Optics. SPIE Field Guides vol. FG01. SPIE. с. 5–20. ISBN 0-8194-5294-7.
  2. Welford, W.T. (1986). Aberrations of Optical Systems. CRC. ISBN 0-85274-564-8.
  3. Hecht, Eugene (2002). Optics (вид. 4th). Addison Wesley. с. 155. ISBN 0-321-18878-0.
  4. Kerr, Douglas A. (2005). The Proper Pivot Point for Panoramic Photography (PDF). The Pumpkin. Архів оригіналу за 13 травня 2006. Процитовано 5 March 2006.
  5. van Walree, Paul. Misconceptions in photographic optics. Архів оригіналу за 19 квітня 2015. Процитовано 1 January 2007. Item #6.
  6. Littlefield, Rik (6 February 2006). Theory of the "No-Parallax" Point in Panorama Photography (pdf). ver. 1.0. Процитовано 14 січня 2007.
  7. Searle, G.F.C. 1912 Revolving Table Method of Measuring Focal Lengths of Optical Systems in "Proceedings of the Optical Convention 1912" p.168-171.
  8. Gray, Henry (1918). Anatomy of the Human Body. с. 1019. Процитовано 12 лютого 2009.

Посилання
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.