Квадрупольна іонна пастка
Квадрупольна іонна пастка, радіочастотна пастка або пастка Пауля — різновид іонної пастки, в якій для уловлювання заряджених частинок використовується змінне електричне поле. Цей тип пастки винайшов Вольфганг Пауль[1][2], за що розділив Нобелівську премію з фізики 1989 року[3]. Пастка Пауля використовується як складова мас-спектрометрів та в квантових комп'ютерах на захоплених іонах.
Засади
Заряджена частинка, наприклад іон атома або молекули, реагує на електричне поле. Неможливо створити таку статичну конфігурацію електричних полів, що обмежувала б рух зарядженої частинки в усіх трьох напрямках (це твердження відоме як теорема Ерншоу). Однак, можливо створити середню силу такого обмеження, використовуючи змінне в часі електричне поле. Для цього потрібно перемикати обмежувальне й антиобмежувальне поле швидше ніж частинка втекла б з пастки. Відповідні пастки часто називають радіочастотними оскільки частота перемикання лежить у радіодіапазоні.
Найпростішою геометрією електричного поля в такій пастці є квадруполь, хоча у спеціалізованих пристроях можуть використовуватися складніші геометрії. Електричні поля створюються електродами. Досконалий квадруполь створюється гіперболічними електродами, хоча іноді заради простоти виготовлення використовуються циліндричні електроди. Існують мікроскопічні іонні пастки, в яких електроди розміщені в одній площині, а область утримання — над цією площиною[4]. Пастки можна розділити на два класи, залежно від того, чи коливання поля забезпечують утримання в трьох чи двох вимірах. У двовимірному випадку (так званій лінійній радіочастотній пастці), обмеження руху частинки в третьому напрямку забезпечується статичним електричним полем.
Починаючи з середини 1980-их у більшості пасток Паулі використовується гелій з тиском приблизно ~1 міліторр. Використання газу та моди селективної за масою нестабільності, розробленої Стаффордом зі співробітниками привело до появи перших комерційних тривимірних пасток[5].
Теорія
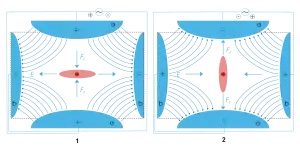
Тривимірна пастка зазвичай складається з двох гіперболічних металевих кінцевих електродів, фокуси яких лежать навпроти один одного, та гіперболічного кільцевого електрода посередині. Іони захоплюються в області між трьома електродами змінними та постійними електричними полями. Напруга змінного радіочастотного сигналу подається на кінцеві електроди, якщо бажано збудити іони, змінна напруга подається на кільцевий електрод. Хмарка іонів на одному півперіоді змінного поля розтягається вздовж осі, і згущується в радіальній площині. Потім, на іншому півперіоді, електричні сили розтягають хмарку іонів у радіальній площині й згущують вздовж осі. Тобто іони здійснюють складний рух, їхня хмарка то видовжується, то звужується почергово в різних напрямках.
Інтуїтивне пояснення та наближення найнижчого порядку аналогічне жорсткому фокусуванню в фізиці прискорювачів. Оскільки сила змінює прискорення, положення відстає на півперіода (в наближенні найнижчого порядку). Частинки дефокусовані тоді, коли сила фокусована, і навпаки. Частинки, що перебувають далі від центра відчувають сильніше поле, коли поле фокусоване, ніж коли воно розфокусоване.

Квадрупольна іонна пастка має дві головні конфігурації: описана тривимірна та лінійна, що використовує 4 паралельні електроди. Використовується також спрощена прямокутна конфігурація[6]. Перевага лінійного дизайну в тому, що збільшується кількість захоплених іонів (зокрема при доплерівському охолодженні) та в простоті, але вона накладає додаткові обмеження на моделювання. Пастка Пауля сконструйована так, щоб створити сідлову точку в конфігурації поля, але у випадку квадруполя ця сідлова точка не може обертатися навколо іона в центрі пастки. Вона може лише змінювати напрямок поля. Через це рух іона в пастці описується рівнянням Матьє, яке можна розв'язати тільки чисельно.
Рівняння руху
У полі квадруполя на іони діє сила, що повертає їх до центру пастки. Рух іонів у змінному силовому полі описується розв'язками рівняння Матьє[7]. Його загальна форма, записана в безрозмірних змінних, має вигляд
Для виводу цього рівняння треба розглянути силу, що діє на іон. Наприклад, в напрямку осі х ця сила дорівнює
де — потенціал електричного поля, — маса іона, — елементарний електричний заряд. Длі квадрупольної пастки потенціал задається формулою:
де — зовнішній потенціал, , та — певні коефіцієнти, що задають конфігурацію поля, а — стала з розмірністю довжини. Для іонної пастки , а , для квадрупольного фільтра маси , .
Зовнішній потенціал є сумою постійної та змінної частин
де — циклічна частота змінної частини потенціалу.
Рівняння руху іона вздовж осі х набирає форми
що має вигляд рівняння Матьє. Аналогічні рівняння можна отримати для руху вздовж інших осей.
Зведення рівняння до канонічної форми рівняння Матьє визначає його коефіцієнти;
- ,
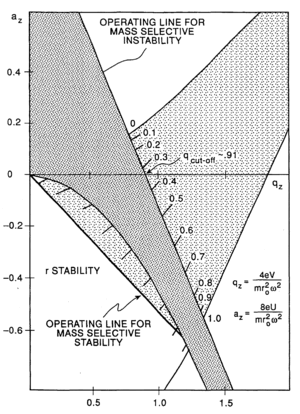
Захоплення іона в пастку можна зрозуміти з аналіз областей стабільності двох рівнянь Матьє — для x-вої та z-вої складових поля в залежності від коефіцієнтів. Цей аналіз проводиться чисельно. Результати продемонстровано на рисунку. Область стабільності — там де перетинаються дві смуги. Деталі можна знайти в книзі Мюллера-Кірстена[8]. Тобто, для успішного захоплення іонів потрібно підібрати параметри потенціалів, розміри системи та частоту.
Інші конфігурації радіочастотних іонних пасток
.jpg.webp)
Лінійна іонна пастка використовує квадрупольні стрижні для обмеження руху іонів у площині перерізу та статичне поле кінцевих електродів для обмеженні їхнього руху вздовж осі[9]. Лінійна форма дозволяє їй працювати як селективний фільтр мас або як пастка, для чого створюється потенціальна яма вздовж осі[10]. Перевагами лінійної пастки є збільшення кількості іонів, які можна утримувати, швидше сканування та простота конструкції (хоча юстування квадрупольних стрижнів критично важливе, що вимагає контролю якості при виробництві додатково до складності виробництва деталей для тривимірних пасток)[11].
Розроблені й виготовляються пастки з циліндричними, а не гіперболічними електродами[12][13][14][15][16]. Структури з таких мікропасток використовуться при розрозбці мініатюрних мас-спектрометрів для детектування хімічних речовин при медичній діагностиці та в інших потреб.
Комбіновані радіочасткові пастки об'єднують у своїй конструкції іонні пастки Пауля та пастки Пеннінга[17]. Одне з вузьких місць таких пасток є те, що вони можуть утримувати тільки однозарядні іони або іони з однаковими масами. Але в певних застосуваннях на кшталт виробництва антиводню важливо утримувати частинки з дуже різними масами. Для досягнення такої мети вздовж осі накладається однорідне магнітне поле.
Примітки
- Paul W., Steinwedel H. (1953). "Ein neues Massenspektrometer ohne Magnetfeld". RZeitschrift für Naturforschung A 8 (7): 448-450
- Патент "Verfahren zur Trennung bzw. zum getrennten Nachweis von Ionen verschiedener spezifischer Ladung", W. Paul and H. Steinwedel, поданий 24 грудня 1953, пріоритет з 23 грудня 1953
- Wolfgang Paul. Electromagnetic traps for charged and neutral particles. Rev. Mod. Phys. 62: 531–540. Bibcode:1990RvMP...62..531P. doi:10.1103/RevModPhys.62.531.
- S. Seidelin. Microfabricated Surface-Electrode Ion Trap for Scalable Quantum Information Processing. Phys. Rev. Lett. 96: 253003. Bibcode:2006PhRvL..96y3003S. arXiv:quant-ph/0601173. doi:10.1103/PhysRevLett.96.253003.
- Stafford, G. C.; P. E. Kelley; J. E. P. Syka; W. E. Reynolds; J. F. J. Todd (7 September 1984). Recent improvements in and analytical applications of advanced ion trap technology. International Journal of Mass Spectrometry and Ion Processes (Elsevier Science B.V.) 60 (1): 85–98. Bibcode:1984IJMSI..60...85S. doi:10.1016/0168-1176(84)80077-4.
- Ouyang Z, Wu G, Song Y, Li H, Plass WR, Cooks RG (August 2004). Rectilinear ion trap: concepts, calculations, and analytical performance of a new mass analyzer. Anal. Chem. 76 (16): 4595–605. PMID 15307768. doi:10.1021/ac049420n.
- March, Raymond E. (1997). An Introduction to Quadrupole Ion Trap Mass Spectrometry. Journal of Mass Spectrometry 32 (4): 351–369. ISSN 1076-5174. doi:10.1002/(SICI)1096-9888(199704)32:4<351::AID-JMS512>3.0.CO;2-Y.
- H.J.W. Müller-Kirsten, Introduction to Quantum Mechanics: Schrödinger Equation and Path Integral, 2nd ed., World Scientific (2012), Chapter 17 on Periodic Potentials, ISBN 978-981-4397-73-5.
- Douglas DJ, Frank AJ, Mao D (2005). Linear ion traps in mass spectrometry. Mass spectrometry reviews 24 (1): 1–29. PMID 15389865. doi:10.1002/mas.20004.
- Quadrupole ion trap mass spectrometry: a view at the turn of the century, Raymond E. March, International Journal of Mass Spectrometry 200, 2000, pp.285-312
- Schwartz, Jae C.; Michael W. Senko; John E. P. Syka (June 2002). A two-dimensional quadrupole ion trap mass spectrometer. Journal of the American Society for Mass Spectrometry (Elsevier Science B.V.) 13 (6): 659–669. PMID 12056566. doi:10.1016/S1044-0305(02)00384-7.
- Kornienko, O., Reilly, P.T.A., Whitten W.B., Ramsey, J.M. (1999). "Micro ion trap mass spectrometry". Rapid Communications in Mass Spectrometry 13 (1): 50-53
- Ouyang Z, Badman ER, Cooks RG (1999). Characterization of a serial array of miniature cylindrical ion trap mass analyzers. Rapid Communications in Mass Spectrometry 13 (24): 2444–9. PMID 10589092. doi:10.1002/(SICI)1097-0231(19991230)13:24<2444::AID-RCM810>3.0.CO;2-F.
- Patterson GE, Guymon AJ, Riter LS, Everly M, Griep-Raming J, Laughlin BC, Ouyang Z, Cooks RG (2002). Miniature cylindrical ion trap mass spectrometer. Anal. Chem. 74 (24): 6145–53. PMID 12510732. doi:10.1021/ac020494d.
- Kanawati B, Wanczek KP (2007). Characterization of a new open cylindrical ion cyclotron resonance cell with unusual geometry. The Review of scientific instruments 78 (7): 074102. Bibcode:2007RScI...78g4102K. PMID 17672776. doi:10.1063/1.2751100.
- Cruz D, Chang JP, Fico M, Guymon AJ, Austin DE, Blain MG (2007). Design, microfabrication, and analysis of micrometer-sized cylindrical ion trap arrays. The Review of scientific instruments 78 (1): 015107. Bibcode:2007RScI...78a5107C. PMID 17503946. doi:10.1063/1.2403840.
- J. Walz; S. B. Ross; C. Zimmermann; L. Ricci; M. Prevedelli; T. W. Hansch (1996). Confinement of electrons and ions in a combined trap with the potential for antihydrogen production. Hyperfine Interactions 100: 133. Bibcode:1996HyInt.100..133W. doi:10.1007/BF02059938.