Клівер трикутника
Клівер трикутника — це відрізок, одна вершина якого лежить в середині однієї зі сторін трикутника, друга вершина лежить на одній з двох сторін, що залишилися, при цьому клівер розбиває периметр навпіл. Крім того, клівер паралельний бісектрисі, проведеній з протилежного до сторони кута, в середині якої бере початок клівер (див. перший малюнок)[1][2].
Властивості
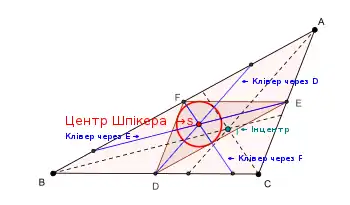
Центр Шпікера трикутника є центром перетину трьох кліверів
- Кожен з кліверів проходить через центр мас периметра трикутника , так що всі три клівери перетинаються в центрі Шпікера або .[1][2]
- Клівер паралельний одній бісектрисі відповідного кута.
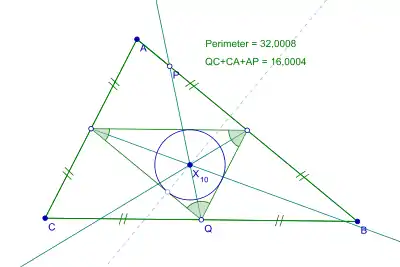
- Клівер розрізає трикутник на дві фігури рівного периметра (див. другий малюнок).
Примітки
- Honsberger, Ross (1995). Chapter 1: Cleavers and Splitters. Episodes in Nineteenth and Twentieth Century Euclidean Geometry. New Mathematical Library 37. Washington, DC: Mathematical Association of America. с. 1–14. ISBN 0-88385-639-5. MR 1316889.
- Avishalom, Dov (1963). The perimetric bisection of triangles. Mathematics Magazine 36 (1): 60–62. JSTOR 2688140. MR 1571272.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.