Центр Шпікера

Центр Шпікера — чудова точка трикутника, яка визначається як центр мас периметра трикутника; тобто центр ваги однорідного дроту, який проходить по периметру трикутника [1][2].

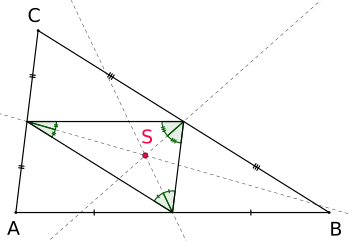
Центр Шпікера є інцентром серединного трикутника

Точку названо на честь німецького геометра XIX століття Теодора Шпікера[3]. В Енциклопедії центрів трикутника Кларка Кімберлінга вказана як X(10)[4].

Властивості

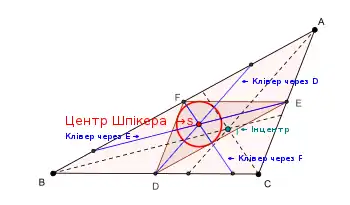
Центр Шпікера (S) трикутника є центром перетину кліверів (позначені синіми лініями).

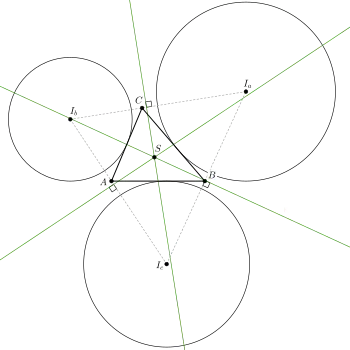
Центр Шпікера

S

— радикальний центр трьох зовнівписаних кіл

\triangle ABC

. Зеленим кольором позначено радикальні осі відповідних пар кіл; вони перпендикулярні до ліній центрів.

Центр Шпікера є інцентром серединного трикутника [1]. Тобто центр Шпікера $\triangle ABC$ є центром кола, вписаного в серединний трикутник $\triangle ABC$ (в його додатковий трикутник)[5]. Це коло називають колом Шпікера.

Центр Шпікера є центром кліверів трикутника $\triangle ABC$ [1]. Тобто всі три клівери трикутника перетинаються в одній точці — в центрі Шпікера $S$ . (Клівер трикутника — це відрізок, одна вершина якого міститься в середині однієї зі сторін трикутника, друга вершина міститься на одній з двох інших сторін, при цьому клівер розбиває периметр навпіл.)

Центр Шпікера, інцентр ( $I$ ), центроїд( $G$ ) і точка Наґеля ( $M$ ) Трикутника лежать на одній прямій — на другий прямій Ейлера (прямій Ейлера — Нагеля). Більш того[6],

\left\{{\begin{matrix}IS=SM;\\IG=2GS;\\MG=2IG.\end{matrix}}\right.

Центр Шпікера $\triangle ABC$ $\text{[math]}$ є точкою перетину прямих $AX$ $\text{[math]}$ , $BY$ $\text{[math]}$ і $CZ$ $\text{[math]}$ , де $\triangle XBC$ $\text{[math]}$ , $\triangle YCA$ і $\triangle ZAB$ $\text{[math]}$ — подібні, рівнобедрені і однаково розташовані, побудовані на сторонах трикутника $\triangle ABC$ зовні, мають однаковий кут при основі $\mathrm {arctg} \,\left(\mathrm {tg} \,{\frac {A}{2}}\;\mathrm {tg} \,{\frac {B}{2}}\;\mathrm {tg} \,{\frac {C}{2}}\right)$ $\text{[math]}$ .
- Ця властивість виконується не тільки для центра Шпікера. Наприклад, перша точка Наполеона $N_{1}$ , як і центр Шпікера, є точкою перетину прямих $AX$ , $BY$ і $CZ$ , де $\triangle XBC$ , $\triangle YCA$ і $\triangle ZAB$ — подібні, рівнобедрені й однаково розташовані, побудовані на сторонах трикутника $\triangle ABC$ зовні, мають однаковий кут при основі $30^{\circ }$ .

Honsberger, 1995, с. 3–4.
Kimberling, Clark. Spieker center. Процитовано 5 травня 2012.
Spieker, 1888.
Kimberling, Clark. Encyclopedia of Triangle Centers. Архів оригіналу за 24 листопада 2015. Процитовано 5 травня 2012.
Серединний трикутник даного $\triangle ABC$ називають додатковим трикутником трикутника ABC
A. Bogomolny. Nagel Line from Interactive Mathematics Miscellany and Puzzles. Процитовано 5 травня 2012.
Odenhal, 2010, с. 35–40.

Boris Odenhal. Some triangle centers associated with the circles tangent to the excircles // Forum Geometricorum. — 2010. — Т. 10 (13 лютого).
Theodor Spieker. Lehrbuch der ebenen Geometrie. — Potsdam, Germany, 1888.
Ross Honsberger. Episodes in Nineteenth and Twentieth Century Euclidean Geometry. — Mathematical Association of America, 1995.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.