Коефіцієнт кореляції Пірсона

Коефіцієнт кореляції Пірсона між двома змінними дорівнює коваріації двох змінних, або сумі добутків відхилень, поділеній на добуток їх стандартних відхилень. Нехай, є дві вибірки ${\displaystyle x^{m}=\left(x_{1},\cdots ,x_{m}\right),\;}$ ${\displaystyle y^{m}=\left(y_{1},\cdots ,y_{m}\right);}$ Коефіцієнт кореляції Пірсона розраховують за формулою:

${\displaystyle r_{xy}={\frac {\sum _{i=1}^{m}\left(x_{i}-{\bar {x}}\right)\left(y_{i}-{\bar {y}}\right)}{\sqrt {\sum _{i=1}^{m}\left(x_{i}-{\bar {x}}\right)^{2}\sum _{i=1}^{m}\left(y_{i}-{\bar {y}}\right)^{2}}}}={\frac {cov(x,y)}{\sqrt {s_{x}^{2}s_{y}^{2}}}},}$

де ${\displaystyle {\bar {x}},}$ ${\displaystyle {\bar {y}}}$ — вибіркові середні ${\displaystyle x^{m}}$ і ${\displaystyle y^{m},}$ ${\displaystyle s_{x}^{2},}$ ${\displaystyle s_{y}^{2}}$ — вибіркові дисперсії, ${\displaystyle r_{xy}\in \left[-1,1\right]}$.

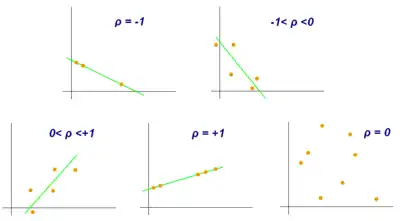
Коефіцієнт кореляції набуває значень від −1 до 1. Значення +1 означає, що залежність між X та Y є лінійною, і всі точки функції лежать на прямій, яка відображає зростання Y при зростанні X. Значення −1 означає, що всі точки лежать на прямій, яка відображає зменшення Y при зростанні X. Якщо коефіцієнт кореляції Пірсона = 0, то саме лінійної кореляції між змінними немає.

Квадрат коефіцієнта кореляції, що є коефіцієнтом детермінації, обчислює частку варіативності змінної Y, яка пояснюється зміною X в простій лінійній регресії. Загальна варіація показників ${\displaystyle Y_{i}}$ відносно їх середнього значення може бути представлена наступним чином:

${\displaystyle \sum _{i}(Y_{i}-{\bar {Y}})^{2}=\sum _{i}(Y_{i}-{\hat {Y}}_{i})^{2}+\sum _{i}({\hat {Y}}_{i}-{\bar {Y}})^{2}}$,

де ${\displaystyle {\hat {Y}}_{i}}$ є середньозваженими значеннями регресії. Застосувавши математичні перетворення, отримаємо:

${\displaystyle 1={\frac {\sum _{i}(Y_{i}-{\hat {Y}}_{i})^{2}}{\sum _{i}(Y_{i}-{\bar {Y}})^{2}}}+{\frac {\sum _{i}({\hat {Y}}_{i}-{\bar {Y}})^{2}}{\sum _{i}(Y_{i}-{\bar {Y}})^{2}}}.}$

Два доданки зверху показують частку варіативності Y, яка пояснюється зміною X (справа) і ту, яка не пояснюється зміною X (зліва).

Далі, ми застосуємо умову методу найменших квадратів, за якою значення коваріації між ${\displaystyle {\hat {Y}}_{i}}$ і ${\displaystyle Y_{i}-{\hat {Y}}_{i}}$ дорівнює нулю. Таким чином, рівняння кореляції між спостережними та середньозваженими значеннями регресії можуть бути записані так:

${\displaystyle {\begin{aligned}r(Y,{\hat {Y}})&={\frac {\sum _{i}(Y_{i}-{\bar {Y}})({\hat {Y}}_{i}-{\bar {Y}})}{\sqrt {\sum _{i}(Y_{i}-{\bar {Y}})^{2}\cdot \sum _{i}({\hat {Y}}_{i}-{\bar {Y}})^{2}}}}\\&={\frac {\sum _{i}(Y_{i}-{\hat {Y}}_{i}+{\hat {Y}}_{i}-{\bar {Y}})({\hat {Y}}_{i}-{\bar {Y}})}{\sqrt {\sum _{i}(Y_{i}-{\bar {Y}})^{2}\cdot \sum _{i}({\hat {Y}}_{i}-{\bar {Y}})^{2}}}}\\&={\frac {\sum _{i}[(Y_{i}-{\hat {Y}}_{i})({\hat {Y}}_{i}-{\bar {Y}})+({\hat {Y}}_{i}-{\bar {Y}})^{2}]}{\sqrt {\sum _{i}(Y_{i}-{\bar {Y}})^{2}\cdot \sum _{i}({\hat {Y}}_{i}-{\bar {Y}})^{2}}}}\\&={\frac {\sum _{i}({\hat {Y}}_{i}-{\bar {Y}})^{2}}{\sqrt {\sum _{i}(Y_{i}-{\bar {Y}})^{2}\cdot \sum _{i}({\hat {Y}}_{i}-{\bar {Y}})^{2}}}}\\&={\sqrt {\frac {\sum _{i}({\hat {Y}}_{i}-{\bar {Y}})^{2}}{\sum _{i}(Y_{i}-{\bar {Y}})^{2}}}}.\end{aligned}}}$

Звідси

${\displaystyle r(Y,{\hat {Y}})^{2}={\frac {\sum _{i}({\hat {Y}}_{i}-{\bar {Y}})^{2}}{\sum _{i}(Y_{i}-{\bar {Y}})^{2}}}}$

Це рівняння показує частку варіативності Y, яка є лінійною функцією X.

Проведені спостереження мають різні ступені важливості, які можуть бути виражені через вектор ваги w. Для обчислення кореляції між векторами x та y з використанням вектора ваги w (для будь-якого n),[6][7]

• Зважена середня:

${\displaystyle \operatorname {m} (x;w)={\sum _{i}w_{i}x_{i} \over \sum _{i}w_{i}}.}$

• Зважена коваріація:

${\displaystyle \operatorname {cov} (x,y;w)={\sum _{i}w_{i}(x_{i}-\operatorname {m} (x;w))(y_{i}-\operatorname {m} (y;w)) \over \sum _{i}w_{i}}.}$

• Зважена кореляція:

${\displaystyle \operatorname {corr} (x,y;w)={\operatorname {cov} (x,y;w) \over {\sqrt {\operatorname {cov} (x,x;w)\operatorname {cov} (y,y;w)}}}.}$

• Часовий ряд