Коло дев'яти точок

Коло дев’яти точок — це коло, яке можна побудувати для будь-якого трикутника. Так називається воно через те, що воно проходить через дев’ять важливих точок, шість з яких лежать на самому трикутнику (за винятком тупокутних трикутників). Ці точки:

Середина кожної сторони трикутника
Основа кожної висоти
Середини відрізків, що сполучають вершини трикутника з ортоцентром

Дев’ять точок

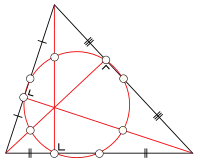
Коло дев’яти точок також відоме як коло Феєрбаха або коло Ейлера.

Доведення теореми про Коло 9 точок

Малюнок 2

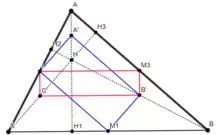
Доведемо тепер, що точки $H_{1}H_{2}H_{3}$ (основи висот), $A'B'C'$ (середини відрізків, що сполучають ортоцентр та вершини трикутника) та $M_{1}M_{2}M_{3}$ (основи медіан) лежать на одному колі (рис. 2). З'єднаємо точки $M_{2}$ та $A'$ , $M_{2}$ та $M_{1}$ , $M_{1}$ та $B'$ , $B'$ та $A'$ , тоді отримаємо паралелограм $M_{2}A'B'M_{1}$ , тому що $A'B'$ серединна лінія в трикутнику $ABC$ тобо $A'B'$ паралельна $AB$ . $M_{1}M_{2}$ серединна лінія в трикутнику $ABC$ звідси випливає, що $A'B'$ прарельно $M_{1}M_{2}$ . Аналогічним чином доводиться, що $A'M_{2}$ паралельно $B'M_{1}$ , але також паралельно висоті $CH_{3}$ , тоді $\angle M_{2}C'B'$ = 90^о звідси випливає, що $\angle B'M_{2}M_{1}$ = 90^о. Тобто паралелограм є прямокутником. Тепер з'єднаємо точки $M_{2}$ та $C'$ , $C'$ та $B'$ , $B'$ та $M_{3}$ , $M_{3}$ та $M_{2}$ . Так само отримаємо, що $M_{2}B'C'M_{3}$ прямокутник. У цих прямокутниках дві спільні вершини, тобто ці прямокутники лежать на одному колі, бо в них спільний діаметр. Ми довели, що середини відрізків отриманих сполученням ортоцентра та вершин трикутника та основи медіан належать одному колу. Зараз доведемо, що основи висот також належать цьому колу. $\angle A'H_{1}M_{1}$ = 90^о та спирається на діаметр (бо діагоналі в прямокутниках – є діаметрами кола, що описане навколо прямокутника) кола утвореного з середини відрізків отриманих сполученням ортоцентра та вершин трикутника, та основ медіан, тобто точка $H_{1}$ лежить на колі. Аналогічним чином доводиться, що основи висот $H_{2}H_{3}$ також належать цьому колу.

Теорема Феєрбаха

Теорема Феєрбаха стверджує, що

Коло дев'яти точок довільного трикутника дотикається до вписаного кола і всіх трьох зовнівписаних кіл цього трикутника.

Ця теорема була сформульована і доведена Карлом Вільгельмом Феєрбахом в 1822-у році.

Посилання

Weisstein, Eric W. Коло дев’яти точок(англ.) на сайті Wolfram MathWorld.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.