Координатний спуск
Координатний спуск — це алгоритм оптимізації, який послідовно мінімізує уздовж координатних напрямків, щоб знайти мінімум функції. При кожній ітерації алгоритм визначає координату або координатний блок за допомогою правила вибору координат, а потім точно або приблизно мінімізує відповідну координатну гіперплощину, фіксуючи всі інші координати або блоки координат. Лінійний пошук по напрямку координат може бути здійснений на поточній ітерації для визначення відповідного розміру кроку. Координатний спуск може застосовуватися як у диференційованому, так і в похідному контексті.
Опис
Координатний спуск заснований на ідеї, що мінімізація багатоваріантної функції може бути досягнута шляхом мінімізації її по одному напрямку за один раз, тобто, вирішення одноманітної (або, принаймні, набагато простішої) проблеми оптимізації в циклі.[1] У найпростішому випадку циклічного координатного спуску, він циклічно повторюється через напрямки, по одному, мінімізуючи цільову функцію щодо кожного напрямку координат одночасно. Тобто, починаючи з початкових значень змінних
крок задає з ітеративно розв'язує проблеми оптимізації єдиної змінної
для кожної змінної з для від 1 до .
Таким чином, починаючи з початкової догадки для локального мінімуму функції , і отримуючи ітеративно послідовність
Використовуючи лінійний пошук кожної ітерації, ми автоматично отримуємо, що
Тут можна побачити що ця послідовність має схожі збіжні властивості як і метод найбільш крутого спуску. Відсутність вдосконалення після одного циклу лінійного пошуку вздовж координатних напрямків вказує на те, що стаціонарна точка досягнута. Цей процес ілюстрований нижче.
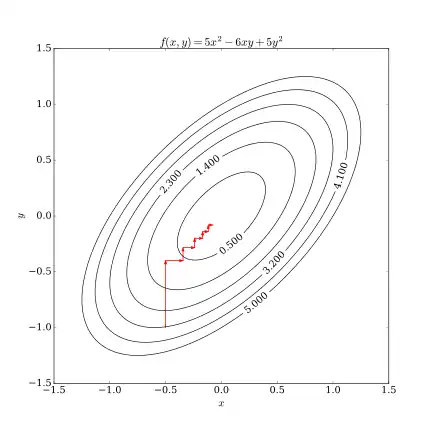
Диференційований випадок
У випадку неперервно диференційованої функції , алгоритм координатного спуску може бути представлений як:[1]
- Виберіть початковий параметричний вектор .
- До тих пір, поки не буде досягнута збіжність або для певної кількості ітерацій:
- Виберіть індекс від 1 до .
- Виберіть розмір кроку .
- Оновлюйте до
Розмір кроку може бути вибраний різними способами, наприклад, шляхом вирішення точного мінімізатора (тобто, зі всіма змінними, але фіксованими ), або за традиційними критеріями пошуку рядків.[1]
Обмеження
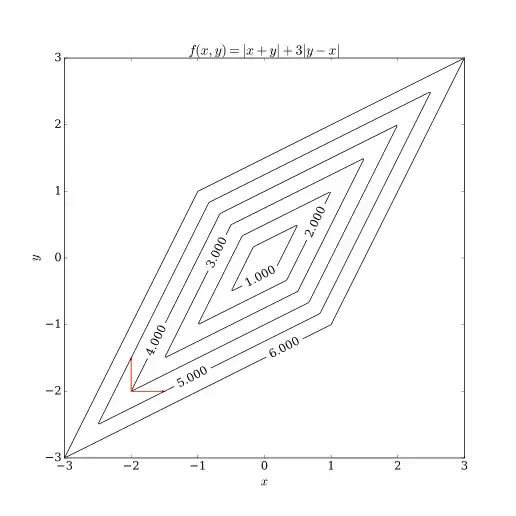
Координатний спуск має дві проблеми. Одна з них — це відсутність гладкої функції багатьох змінних. На наступному малюнку видно, що ітеративний спуск координатами може застрягнути в нестаціонарній точці, якщо криві рівня функції не є гладкими. Припустимо, що алгоритм знаходиться в точці (-2, -2); Тоді є два напрями, орієнтовані на осі, які можна розглянути для кроку, позначені червоними стрілками. Однак кожен крок уздовж цих двох напрямків збільшуватиме значення цільової функції (припускаючи проблему мінімізації), тому алгоритм не зробить жодного кроку, навіть якщо обидва кроки разом наблизили б алгоритм до оптимального. Хоча цей приклад показує, що спуск координатами не обов'язково збігається з оптимальним, можливо виявити формальне зближення при розумних умовах.[2]
Інша проблема — це складність розпаралелювання даного алгоритму. Оскільки суть координатного спуску полягає у проходженні напрямків та мінімізації цільової функції стосовно кожного координатного напрямку, спуск координат не є тривіальною задачею для паралелізму. Останні дослідницькі роботи показали, що паралелізм застосовується для координатного спуску шляхом послаблення зміни цільової функції стосовно кожного координатного напрямку.[3][4][5]
Застосування
Алгоритми координатного спуску користуються популярністю у практикантів завдяки своїй простоті, але та сама властивість змусила дослідників оптимізації значною мірою ігнорувати їх на користь більш цікавих (складних) методів. Раннє застосування оптимізації методом спуску координат було в області комп'ютерної томографії[6], де було виявлено швидку збіжність[7], а згодом було використано для клінічної реконструкції багатоклітинної спіральної томографії[8]. Крім того, виявився підвищений інтерес до використання координатного спуску з появою масштабних проблем у машинному навчанні, коли спуск координат виявився конкурентоспроможним для інших методів при застосуванні до таких проблем, як навчання лінійних методу опорних векторів[9] і розкладу невід'ємних матриць[10]. Вони привабливі для проблем, коли обчислення градієнтів недосяжно, можливо, тому, що дані, необхідні для цього, поширюються по комп'ютерних мережах.[11]
Примітки
- Wright, Stephen J. (2015-06). Coordinate descent algorithms. Mathematical Programming (англ.) 151 (1). с. 3–34. ISSN 0025-5610. doi:10.1007/s10107-015-0892-3. Процитовано 23 грудня 2019.
- Spall, James C. (2012-07). Cyclic Seesaw Process for Optimization and Identification. Journal of Optimization Theory and Applications (англ.) 154 (1). с. 187–208. ISSN 0022-3239. doi:10.1007/s10957-012-0001-1. Процитовано 23 грудня 2019.
- Zheng, J.; Saquib, S.S.; Sauer, K.; Bouman, C.A. (2000). Parallelizable Bayesian tomography algorithms with rapid, guaranteed convergence. IEEE Transactions on Image Processing 9 (10). с. 1745–1759. ISSN 1057-7149. doi:10.1109/83.869186. Процитовано 23 грудня 2019.
- Fessler, J.A.; Ficaro, E.P.; Clinthorne, N.H.; Lange, K. (1997-04). Grouped-coordinate ascent algorithms for penalized-likelihood transmission image reconstruction. IEEE Transactions on Medical Imaging 16 (2). с. 166–175. ISSN 0278-0062. doi:10.1109/42.563662. Процитовано 23 грудня 2019.
- Sabne, Amit; Wang, Xiao; Kisner, Sherman J.; Bouman, Charles A.; Raghunathan, Anand; Midkiff, Samuel P. (2017). Model-based Iterative CT Image Reconstruction on GPUs. Proceedings of the 22nd ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming - PPoPP '17 (ACM Press). ISBN 978-1-4503-4493-7. doi:10.1145/3018743.3018765. Процитовано 23 грудня 2019.
- Sauer, K.; Bouman, C. (1993). A local update strategy for iterative reconstruction from projections. IEEE Transactions on Signal Processing 41 (2). с. 534–548. ISSN 1053-587X. doi:10.1109/78.193196. Процитовано 23 грудня 2019.
- Yu, Zhou; Thibault, Jean-Baptiste; Bouman, Charles A.; Sauer, Ken D.; Hsieh, Jiang (2011-01). Fast Model-Based X-Ray CT Reconstruction Using Spatially Nonhomogeneous ICD Optimization. IEEE Transactions on Image Processing 20 (1). с. 161–175. ISSN 1057-7149. doi:10.1109/tip.2010.2058811. Процитовано 23 грудня 2019.
- Thibault, Jean-Baptiste; Sauer, Ken D.; Bouman, Charles A.; Hsieh, Jiang (29 жовтня 2007). A three-dimensional statistical approach to improved image quality for multislice helical CT. Medical Physics 34 (11). с. 4526–4544. ISSN 0094-2405. doi:10.1118/1.2789499. Процитовано 23 грудня 2019.
- Hsieh, Cho-Jui; Chang, Kai-Wei; Lin, Chih-Jen; Keerthi, S. Sathiya; Sundararajan, S. (2008). A dual coordinate descent method for large-scale linear SVM. Proceedings of the 25th international conference on Machine learning - ICML '08 (ACM Press). ISBN 978-1-60558-205-4. doi:10.1145/1390156.1390208. Процитовано 23 грудня 2019.
- Hsieh, Cho-Jui; Dhillon, Inderjit S. (2011). Fast coordinate descent methods with variable selection for non-negative matrix factorization. Proceedings of the 17th ACM SIGKDD international conference on Knowledge discovery and data mining - KDD '11 (ACM Press). ISBN 978-1-4503-0813-7. doi:10.1145/2020408.2020577. Процитовано 23 грудня 2019.
- Nesterov, Yu. (2012-01). Efficiency of Coordinate Descent Methods on Huge-Scale Optimization Problems. SIAM Journal on Optimization 22 (2). с. 341–362. ISSN 1052-6234. doi:10.1137/100802001. Процитовано 23 грудня 2019.