Система координат
Система координат — спосіб задання точок простору за допомогою чисел. Кількість чисел, необхідних для однозначного визначення будь-якої точки простору, визначає його вимірність. Обов'язковим елементом системи координат є початок координат — точка, від якої ведеться відлік відстаней. Іншим обов'язковим елементом є одиниця довжини, яка дозволяє відраховувати відстані. Всі точки одновимірного простору можна задати при обраному початку координат одним числом. Для двовимірного простору необхідні два числа, для тривимірного — три. Ці числа називають координатами.
Координати на площині і в тривимірному просторі можна задавати багатьма різними способами. Розв'язуючи ту або іншу математичну або фізичну задачу, можна застосовувати різні координатні системи, обираючи з них ту, в якій завдання розв'язується простіше або зручніше в даному конкретному випадку.
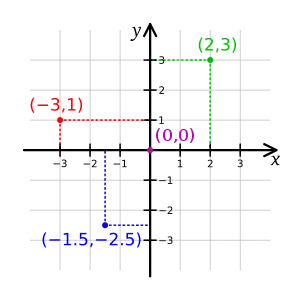
Системи координат в елементарній геометрії — величини, що визначають положення точки на площині і в просторі. На площині положення точки найчастіше визначається відстанями від двох прямих (координатних осей), що перетинаються в одній точці (початку координат) під прямим кутом; одна з координат називається ординатою, а інша — абсцисою. У просторі за системою Декарта положення точки визначається відстанями від трьох площин координат, що перетинаються в одній точці під прямими кутами одна до одної, або сферичними координатами, де початок координат перебуває в центрі сфери.
Історія
Розвиток систем координат в історії людства пов'язаний як з математичними задачами, так і з практичними проблемами мистецтва навігації, що спиралася на картографію та астрономію. Найвідомішу систему координат, прямокутну, запропонував Рене Декарт у 1637 році. Поняття про полярну систему координат у європейській математиці склалося приблизно в ці ж часи, але перші у'являння про неї існували ще в Стародавній Греції, у середньовічних арабських математиків, які розробляли методи обрахунку напрямку на Каабу.
Становлення поняття систем координат призвело до розвитку нових розділів геометрії: аналітичної, проєктивної, нарисної.
Декартова система координат
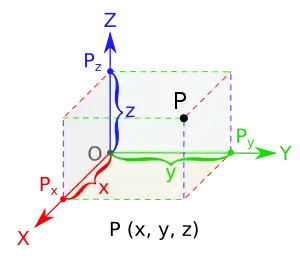
Найпоширенішою системою координат у математиці є декартова система координат, названа так на честь Рене Декарта. Декартова система координат задається початком координат і трьома векторами, які визначають напрям координатних осей. Кожна точка простору задається числами, які дорівнюють віддалі від даної точки до координатних площин.
У двововимірній системі Декартових координат, розташування точки P на xy-площині визначається парою чисел .
- — відстань від точки P до осі y або значення абсциси (з урахуванням знаку)
- — відстань від точки P до осі x або значення ординати (з урахуванням знаку)
В тривимірній системі Декартових координат, точка P в xyz-просторі локалізується вже за допомогою трьох параметрів: .
- — відстань від точки P до площини yz
- — відстань від точки P до площини xz
- — відстань від точки P до площини xy
Різні декартові системи координат зв'язані між собою афінними перетвореннями: зсувом і поворотами.
Криволінійні системи координат
Виходячи з декартової системи координат, можна визначити криволіну систему координат, тобто, наприклад, для тривимірного простору числа , зв'язаних із декартовими координатами співідношеннями:
- ,
де всі функції однозначні й неперервно диференційовані, причому якобіан:
- .
Властивості
Кожне з рівнянь , задає координатну площину. Перетин двох координатних площин із різними i задає координатну лінію. Кожна точка простору визначається перетином трьох координатних площин.
Важливими характеристиками криволінійних систем координат є довжина елемента дуги й елемента об'єму у них. Ці величини використовуються при інтегруванні. Довжина елементу дуги задається квадратичною формою:
- ,
де
є компонентами метричного тензора.
Елемент об'єму дорівнює в криволінійній системі координат
- .
Квадрат якобіана дорівнює детермінанту від метричного тензора:
- .
Система координат називається правою, якщо дотичні до координатних ліній, направлені в бік зростання відповідних координат, утворюють праву трійку векторів.
При описі векторів у криволінійній системі координат зручно користуватися локальним базисом, визначеним у кожній точці.
Полярна система координат
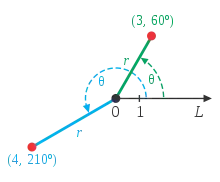
Прикладом криволінійної системи координат на площині є полярна система координат, в якій положення точки задається двома числами: відстанню між точкою та початком координат, і кутом між променем, який сполучає початок координат із точкою та обраною віссю. Декартові та полярні координати точки зв'язані між собою формулами:
- ,
- ,
Деякі рівняння в полярній системі координат мають простіший вигляд (конічні перетини, спіралі, кардіоїда, тощо). Полярну систему координат можна узагальнити на випадок n-вимірного простору. Випадок n=2 (на площині) відповідає звичайній полярній системі координат, а n=3 — сферичній системі координат.
Циліндрична система координат
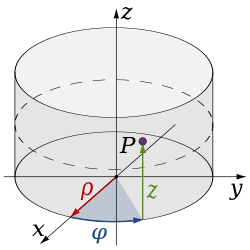
Циліндричні координати — тривимірний аналог полярних, у якому розташування точки P подається впорядкованою трійкою параметрів У термінах декартової системи координат:
- (радіус) — відстань від осі z до точки P,
- (азимут або довгота) — кут між податною («плюсовою») частиною осі x і відрізком, проведеним від полюса до точки P й спроектованим на площину xy.
- (висота), що відповідає декартовій z — координаті точки P.
- Примітка: у літературі для першої (радіальної) координати іноді застосовується позначення ρ, для другої (кутової, чи азимутальної) — позначення θ, для третьої координати — позначення h.
Циліндричні координати є корисними для вивчення систем, симетричних відносно деякої осі. Наприклад, довга циліндрична поверхня з радіусом R у декартових координатах (з віссю z, яка збігається з віссю циліндра) описується рівнянням тоді як у циліндричних координатах воно має суттєво простіший вигляд, як r = R.
Сферична система координат
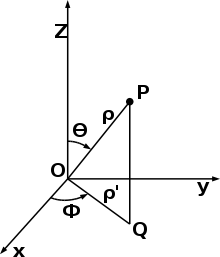
У сферичній системі координат розташування точки P визначається трьома компонентами: У термінах декартової системи координат:
- (радіус) — відстань від точки P до полюса,
- (азимут або довгота) — кут між додатною піввіссю x і проекцією відрізка, проведеного з полюса до точки P, на площину xy.
- (широта або полярний кут) — кут між додатною піввіссю z і відрізком, проведеним з полюса до точки P.
- Примітка: в літературі іноді азимут позначається θ, а полярний кут — φ. Інколи для радіальної координати використовується r замість ρ. Крім того, діапазон кутів для азимута може обиратись як (−180°, +180°] замість діапазона [0°, +360°). Нарешті, полярний кут може мати відлік не від додатного напрямку осі z, а від площини xy; у цьому випадку віл лежить у діапазоні [−90°, +90°], а не у діапазоні [0°, 180°]. Іноді порядок координат у трійці обирається іншим від описаного; наприклад, полярний і азимутальний кути можуть переставлятись.
Сферична система координат також має недолік: φ і θ є не визначеними, якщо ρ = 0; кут φ є не визначеним також и для граничних значень θ = 0 і θ = 180° (або для θ = ±90°, для випадку прийняття відповідного діапазону для цього кута).
Сферичні координати є корисними при вивченні систем, симетричних відносно точки. Так, рівняння сфери з радіусом R у декартових координатах з початком відліку у центрі сфери записується як тоді як у сферичних координатах воно стає набагато простішим:
Положення літака в просторі можна задати трьома числами: висотою, відстанню від деякої точки на поверхні Землі та кутом між напрямком на літак і напрямком на північ. Таке задання відповідає циліндричній системі координат. Альтернативно, положення літака можна задати відстанню до нього та двома кутами: полярним та азимутальним. Таке задання відповідає сферичній системі координат.
Перехід від однієї системи координат до іншої
Декартові та полярні
де u0 — функція Гевісайда з , а sgn — функція signum. Тут функції u0 та sgn використовуються як «логічні» перемикачі, аналогічні за значенням операторам «якщо..то» (if…else) в мовах програмування. Деякі мови програмування мають спеціальну функцію atan2(y, x), яка знаходить вірне значення θ в необхідному квадранті, визначеному x та y.
Декартові та циліндричні
Декартові та сферичні
Циліндричні та сферичні
Застосування
Застосування в географії
У географії та картографії положення на місцевості визначають трьома числами: широтою, довготою і висотою над відомим загальним рівнем (найчастіше, wt рівень моря). Перші два числа є кутами, і визначення відстаней за ними опирається на відоме значення радіуса Землі.
На мапах зазвичай позначаються лінії паралелей та меридіанів, а також масштаб, за яким зручно визначати відстані. Висота над рівнем моря на картах зображують ізогіпсами (горизонталями).
Застосування в астрономії
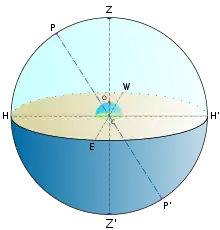
В астрономії за допомогою координат визначають положення зір і допоміжних точок на небосхилі. В астрономії користуються різними системами небесних координат. Кожна з них по суті є сферичною системою координат, в якій відстань до об'єкта спостереження іноді лишається невідомою. Систему небесних координат задають великим колом небесної сфери (або його полюсом, віддаленим на 90° від будь-якої точки цього кола) із вказівкою на цьому колі початкової точки (від якої відлічують інші координати) та напрямку їх відліку. Залежно від вибору фундаментального кола застосовують такі системи небесних координат[1]:
- горизонтальна система координат — головною площиною є справжній (математичний) горизонт, виділеним напрямком — південь.
- екваторіальна система координат — головною площиною є площина земного екватора, на якій виділяють точку весняного рівнодення, в якій екватор перетинається з екліптикою.
- екліптична система координат — головною площиною є екліптика, на якій виділено точку весняного рівнодення, де екватор перетинається з екліптикою.
- галактична система координат — головною площиною є галактична площина, а виділеним напрямком — напрямок на галактичний центр.
Застосування у фізиці
Різноманітність систем координат не вичерпується вищенаведеними. Існує дуже багато криволінійних систем координат, зручних для розв'язування тієї чи іншої задачі. Наприклад, для тривимірного простору іноді застосовують циліндричну систему координат.
Описуючи рух фізичних тіл, фізика використовує поняття системи відліку. Система відліку потребує окрім задання просторової системи координат, додаткового числа, яким вимірюється час. Три просторові та одна часова координата утворюють так званий простір-час. Початок відліку системи координат у фізиці зазвичай пов'язується з якимсь тілом, яке в обраній системі координат вважається нерухомим. Обрання початку координат не є однозначним. Так, наприклад, можна обрати за початок координат центр Землі. Тоді Земля буде вважатися нерухомою. Однак, можна обрати за початок координат барицентр Сонячної системи, і в цій системі координат Земля буде рухатися по еліптичній орбіті.
Загальний принцип фізики, принцип відносності, вимагає, щоб формулювання всіх фізичних законів не залежало від обраної системи відліку. Це положення лежить в основі теорії відносності. Іншим важливим положенням теорії відносності є принцип близькодії, за яким існує максимальна швидкість передачі сигналів, яку називають швидкістю світла. Значення швидкості світла, як і вимагає принцип відносності, не залежить від системи відліку.
Див. також
Примітки
- Небесні координати // Астрономічний енциклопедичний словник / за заг. ред. І. А. Климишина та А. О. Корсунь. — Львів : Голов. астроном. обсерваторія НАН України : Львів. нац. ун-т ім. Івана Франка, 2003. — С. 314—316. — ISBN 966-613-263-X.
Джерела
- Корн Г., Корн Т. Справочник по матиматике. — М.: Наука, 1974. — 832 с.(С. 519) (рос.)
