Локально лінійно зв'язаний простір

Локально лінійно зв'язаний простір — топологічний простір, в якому для будь-якої точки і будь-якого її околу є менший лінійно зв'язаний відкритий окіл. Іншими словами, для кожної точки знайдеться база околів, що складається з лінійно зв'язаних множин.

Підмножина топологічного простору називається локально лінійно зв'язаною, якщо воно разом зі своєю індукованої топологією утворює локально лінійно зв'язаний простір.

Властивості

Локально лінійно зв'язний простір є локально зв'язаним, обернене твердження не є вірним.
Зв'язаний, локально лінійно зв'язний простір є лінійно зв'язаним.
Відкрита підмножина локально лінійно зв'язаного простору теж є локально лінійно зв'язаним простором.
Топологічний простір є локально лінійно зв'язаним тоді і тільки тоді коли для довільної його відкритої підмножини її компоненти лінійної зв'язності є відкритими підмножинами.
У локально лінійно зв'язаних просторів поняття компонент зв'язності і компонент лінійної зв'язності є еквівалентними.
Більшість основних теорем теорії накриттів, зокрема існування універсального накриття вимагає щоб базовий простір був лінійно зв'язаним, локально лінійно зв'язаним і напівлокально однозв'язним.

Приклади

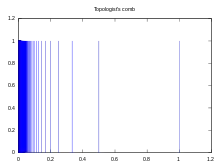
Топологічний гребінь.

Евклідів простір $\mathbb {R} ^{n}$ зі стандартною топологією є локально лінійно зв'язаним.
Простір $[0,1]\cup [2,3]$ з топологією, індукованої стандартною топологією дійсної прямої, є локально лінійно зв'язаним, однак не є лінійно зв'язаним.
Підмножина евклідової площини $\left(\{0\}\times [0,1]\right)\cup \left([0,1]\times \{0\}\right)\cup \left(\{1/n\mid n\in \mathbb {N} \}\times [0,1]\right)$ з топологією, індукованої стандартною топологією, є, очевидно, лінійно зв'язаним простором, проте не локально лінійно зв'язаним (будь-який відкритий окіл точки $(0,1/2)$ не є лінійно зв'язаним).
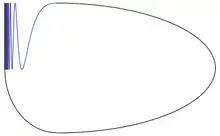
Іншим прикладом простору, що є лінійно зв'язаним але не є локально лінійно зв'язаним є об'єднання графіка функції $\sin(1/x),\;x\in (0,1/\pi ]$ із дугою,що сполучає точки (1,0) і (0,-1). Будь-який відкритий окіл точки $(0,-1)$ не є лінійно зв'язаним
Зліченна множина з кофінітною топологією (замкнутими підмножинами якої є скінченні підмножини весь простір) є локально зв'язаним простором, але не є локально лінійно зв'язаним.

Див. також

Література

Gaal, Steven A.(1966), Point set topology, New York: Dover Publications, ISBN 978-0-486-47222-5 (англ.)
Isadore Singer, John A. Thorpe (1967), Lecture Notes on Elementary Geometry and Topology, Springer-Verlag ISBN 0-387-90202-3 (англ.)
Steen, Lynn Arthur; Seebach, J. Arthur Jr. (1995) [1978]. Counterexamples in Topology (вид. Dover reprint of 1978). Mineola, NY: Dover Publications, Inc. ISBN 978-0-486-68735-3. MR 1382863.(англ.)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.