Лямбда-куб
Ля́мбда-куб (λ-куб) — наочна класифікація восьми типізованих лямбда-числень з явним приписуванням типів (систем, типізованих за Черчем). Куб організований відповідно до можливих залежностей між типами і термами цього числення і формує природну структуру для числення конструкцій. Ідею λ-куба запропонував 1991 року нідерландський логік і математик Генк Барендрегт. Подальші узагальнення лямбда-куба можна отримати, розглядаючи чисту систему типів.
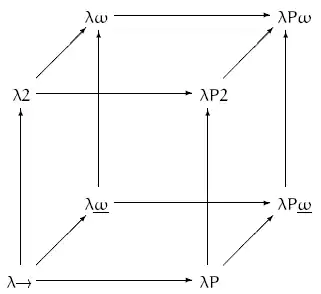
Структура λ-куба
У системах λ-куба змінні відносять до одного з двох сортів: або . Всі допустимі вирази теж поділяються за сортами. Твердження про належність виразу до сорту надбудовується над твердженням типізації, тобто висловлювання читається так: елемент має тип і належить до сорту . Сорт використовується для звичайних змінних і термів λ-числення, сорт — для змінних і виразів типу. Тому в системах λ-куба типи сорту і елементи сорту розглядаються як перетинні. Наприклад, тип терма можна записати як елемент «вищого» сорту . Типи сорту іноді називають родами.
Під залежністю розуміють можливість визначати і використовувати функції, які відбивають елементи одного сорту в інший (або той самий). Елементи сорту залежать від елементів сорту , якщо:
- для допустимого виразу , який, можливо, містить змінну , можна визначити лямбда-абстракцію ;
- для функції має бути допустимим її застосування до елемента , при цьому результат має бути елементом типу сорту , тобто .
Базовою вершиною куба є система , що відповідає просто типізованому лямбда-численню. Терми (елементи сорту ) залежать від термів; типи (елементи сорту ) в залежностях участі не беруть. Три осі, що виходять з базової вершини, породжують такі системи:
- терми, які залежать від типів: система (лямбда-числення з поліморфними типами, система F);
- типи, які залежать від типів: система (лямбда-числення з операторами над типами);
- типи, які залежать від термів: система (лямбда-числення з залежними типами).
Решта систем є різними комбінаціями перелічених залежностей. Найбагатша система (поліморфне лямбда-числення вищого порядку з залежними типами) фактично є численням конструкцій.
Властивості систем λ-куба
Всі системи лямбда-куба мають властивість сильної нормалізації будь-який допустимий терм (і тип) за скінченне число β-редукцій зводиться до єдиної нормальної форми.
Підтримка в мовах програмування
Різні функційні мови підтримують різні підмножини поданих у лямбда-кубі систем типів.
Посилання
- Henk Barendregt, Lambda Calculi with Types(англ.) Handbook of Logic in Computer Science, Volume II, Oxford University Press.
- Simon Peyton Jones and Erik Meijer, 1997.. Henk: A Typed Intermediate Language(англ.)
- Lennart Augustsson, 2007. Simpler, Easier!(англ.) Опис реалізації систем лямбда-куба мовою Haskell.
- Лямбда-куб на SpbHUG(рос.) з перекладом Дениса Москвіна розділу про лямбда-куб із книги Henk Barendregt, Lambda Calculi with Types