Обмеженість функцією

Діаграма проблеми коробки зі свічею

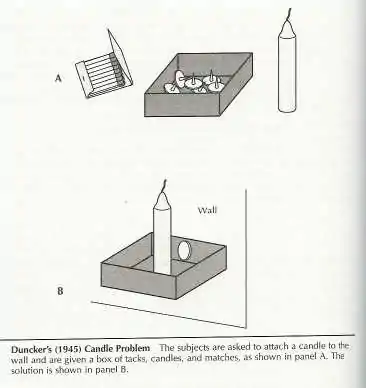
У класичному експерименті на обмеженій функцією 1945 року, Дункер[1] запропонував учасникам свічку, коробку з канцелярськими кнопками та коробку сірників і два завдання закріпити свічу на стіні так, щоб віск не капав на стіл під стіною. Дункер побачив, що учасники намагались прикріпити свічу прямо до стіни канцелярськими кнопками або розтопивши її частину за допомогою сірників. І лише декілька з них здогадались використати нижню частину коробки з канцелярськими кнопками як свічник, прикріпивши її до стіни. За його словами, учасники «зафіксувались» на звичайній функції коробки — містити кнопки, і не могли змінити свою концепцію про коробку, щоб вирішити проблему. Також, учасники вдвічі частіше вирішували проблему, якщо коробку їм видавали пустою, а не з кнопками[3]

У 2003 році Франк та Рамскар[4] запропонували студентам перших курсів Стенфордського університету письмовий варіант цієї задачі з коробкою і свічею. Коли текст був ідентичний оригінальному експерименту, проблему вирішили 23% студентів. У варіанті для другої групи студентів у тексті були підкреслені іменникові словосполучення, напр. «коробка сірників», а для третьої групи були підкреслені іменники (напр., «коробка»). Процент тих, хто ефективно вирішив проблему, зріс до 55% та 47%  відповідно. У повторному експерименті були підкреслені всі іменники крім слова «коробка», і результати були схожі. Автори дійшли висновку, що результат студентів залежав від їх представлення лексичної концепції «коробка», а не від маніпуляцій з інструкцією. Здатність подолати обмеженість функцією залежала від гнучкого представлення слова «коробка», яку дозволило студентами побачити, що коробка може бути використання для закріплення свічі на стіні.

У 1952 році Адамсон[3] повторив експеримент Дункера з коробкою, але розділив учасників на дві експериментальні групу: з попереднім використанням (предмети надаватися учасникам у традиційній манері — всі складені у коробку) та без попереднього використання (матеріали надавалися окремо, тобто коробка була пуста). У другій групі кількість тих, хто задумався про інші використання коробки та вирішив проблему, була вищою.

У 1951 році Бірч та Рабінович[5] пристосували проблему двох мотузок (раніше використану Норманом Маєром у 1930–1931 рр.), за якою учаснику надавалось дві мотузки, закріплені на стелі та два важкі предмети (реле та вимикач). Завдання учасника — зв'язати дві мотузки, але вони досить далеко одна від одної, щоб можна було дотягнутись. Рішення полягало в тому, щоб прив'язати один з важких предметів до мотузки, хитнути як маятник, потім зловити її, тримаючи  в іншій руці другу мотузку, та зв'язати. Учасників поділили на три групи: група R, яка до цього виконувала «розминку» з замикання електричної мережі з використанням реле, група S, яка замикала мережу перемикачем, та група C, яка не мала «розминки». При розв'язанні проблеми учасники групи R частіше як важіль використовували вимикач, групи S — реле. Обидві групи таки робили, бо попередній досвід «привчив» їх до використання предметів певним чином, і обмеженість функцією не дозволила їм побачити інше використання предмету.

Питання барометру — це приклад неправильно сформульованого екзаменаційного питання, що демонструє обмеженість функцією, яка створює моральну дилему для екзаменатора. У класичній формі, популяризованій американським професором- розробником тестів Александром Каландрою  (1911–2006), питання було таке: «продемонструйте, як за допомогою барометра виміряти висоту хмарочосу?»[6] Екзаменатор був впевнений, що на питання є єдина правильна відповідь. Але всупереч його очікуванням, студент дав ряд абсолютно різних відповідей, всі з яких були правильними. При цьому студент не дав відповідь, яка б демонструвала його знання у темі, з якої власне був тест.

Каландра зазначив, що він був свідком цього випадку, і що від відбувся під час Супутникової кризи[7] Його есе «Angels on a Pin» («Ангели на шпильці») було надруковано 1959 у журналі «Pride» PR-асоціації американських коледжів[8], декілька разів передруковувалось у журналах[9][10] та було включено до його книги 1969 року «The Teaching of Elementary Science and Mathematics»[11]. Того ж року воно стало предметом академічної дискусії[12]. З 1970 року[13] проблема увійшла у багато книжок з таких питань як навчання[14], навички письма[15], поради щодо робочого місця,[16] інвестиції у нерухомість[17], хімічна промисловість,[18] програмування,[19] та дизайн мікросхем.[20]

Дослідники вивчали, чи впливає на обмеженість функцією належність до різних культур. 

Нещодавнє дослідження надало попередні докази на користь універсальності обмеженості функцією в різних культурах.[21] Метою дослідження було протестувати людей з неіндустріалізованих суспільств, особливо тих, хто має низький доступ до «високотехнологічних» артефактів, чи вони мають обмеженість функцією. Досліджувався індіанський народ шуари, мисливці-землероби амазонського регіону Еквадору, яких порівнювали з контрольною групою з індустріальної культури.

Спільнота шуар знала лише обмежену кількість індустріальних артефактів — мачете, сокири, казани, цвяхи, рушниці та риболовні гачки, всі з яких вважаються «низькотехнологічними». Учасникам дослідження давали два завдання: завдання з коробкою, в якому учасники повинні були збудувати вежу, щоб допомогли уявному персонажу досягти іншого персонажа, з обмеженим набором різних матеріалів; та завдання з ложкою, в якому учасників просили вирішити проблему з вигаданої історії про кролика, якому треба перебратися на інший берег річки, була збудована «сцена» і учасникам надані різні матеріали, включно з ложкою. У задачі з коробкою, учасники шуар повільніше обирали матеріали, ніж контрольна група, але у часі на вирішення проблеми різниці не було. У завданні з ложкою, учасники шуар повільніше і обирали, і вирішували проблему. Результати показали, що люди неіндустріальних («технологічно обмежених») культур також піддаються обмеженості функцією. Вони швидше використовували предмети без підготовки, ніж коли їм пояснювали основну функцію цих предметів. Це відбувалось незважаючи на те, що вони мають мало доступу до індустріальних промислово вироблених артефактів, а ті, що їм доступні, використовуються ними у різні способи, крім початкового призначення.[21]

Дослідники у двох експериментах вивчали, «чи призведе включення неналежних елементів, разом з інструкцією до проблеми з дизайну, до ефектів фіксації у студентів, які не мають досвіду у дизайнерських завданнях».[22] Вони досліджували включення прикладів неналежних елементів шляхом детального опису проблемних аспектів задачі, запропонованої студентам дизайнами-прикладами. Вони тестували учасників-неекспертів в рамках трьох умов: зі стандартною інструкцією, фіксована (з включенням проблемного дизайну) та дефіксована (з включенням проблемного дизайну, до якого додавались корисні методи). Дослідники змогли підтвердити свою гіпотезу, побачивши в експерименті, що: a) проблемні приклади дизайну створюють суттєві ефекти фіксації, та b) такі ефекти фіксації можна зменшити з використанням дефіксуючих інструкцій.

У «Проблемі одноразового непроливного стаканчика для кави», адаптованої з проблеми Дженсона та Сміта 1991 року, учасників просили створити якомога більше дизайнів недорогого, одноразового, непроливного кавового стаканчика . Учасники групи стандартної умови отримали лише інструкції. Учасники фіксованої умови отримали інструкцію, дизайн та перелік проблем, яких вони мали бути свідомі. А учасники дефіксованої умови отримали все, що інші групи, і на додаток зауваження щодо елементів дизайну, які бажано не використовувати. Інші дві проблеми включали створення вішалки для велосипеда та створення контейнеру для крем-сиру.

За припущення, що студенти відчувають обмеженість функцією, було проведено дослідження з передачі аналогій у науковій аудиторії та отримані дані, які можуть допомогти створити техніку подолання обмеженості функцією. Результати дослідження показують, що студенти демонструють позитивну передачу (покращення) по відношенню до вирішення проблеми після того, як їм надали аналогії певної структури та формату. Це дослідження розширило експерименти Дункера 1945 року, намагаючись продемонструвати, що коли студентам надати одну аналогію у форматі проблеми, замість опису, вони покращать результати вирішення завдань[23].

Всього у дослідженні взяли участь 266 студентів-першокурсників природничих наук. Експеримент проводився у форматі 2x2, де перевірялись умови «контексти завдання» (тип та формат) vs. «попереднього знання» (спеціального vs. загального). Студентів поділили на 5 груп, в чотири з яких студенти потрапили відповідно до рівня їх попередніх наукових знань (від спеціальних до загальних), а одна група була контрольною (без презентації аналогій). Чотири групи потім поділили на умови «аналогія типу та аналогія формату», структурні чи поверхневі типі та формати проблеми чи поверхні.

Було продемонстровано певні невичерпні докази існування позитивної передачі аналогій на основі попереднього знання; однак різні групи мали різний рівень реакції. Формат проблеми та структурний тип презентації аналогій мали найвищу позитивну передачу на вирішення проблем. Дослідники припустили, що добре продумана та спланована аналогія, релевантна за форматом та типом до задачі на вирішення проблеми, може допомогти студентам подолати обмеженість функцією. Результати дослідження можуть бути корисними як для вивчення роботи мозку, так і для покращення навчального процесу[23].

Дослідження Латура 1994 року припустило, що обмеженість функцією можна подолати рішеннями по відношенню до функціонально зафіксованих дизайнів, які зберігають основу дизайну[24]. Це допомагає людині, яка створила функціонально зафіксований дизайн, зрозуміти, як вирішувати загальні проблеми такого типу, а не використовувати створене фіксоване рішення лише для специфічної проблеми. Латур досліджував, як розробники програмного забезпечення аналізують відносно стандартний шматок коду — алгоритм швидкого сортування — і використовують його для створення функції розділення. Частина алгоритму швидкого сортування містить розподіл переліку на частини, щоб його можна було відсортувати; експериментатори хотіли використати код, вже наявний в алгоритмі, лише для розподілу. Для цього вони виділили блоки коду, визначивши їх призначення та вирішивши, чи цей блок необхідний для алгоритму розподілу. Таке абстрагування дозволило їм використати алгоритм швидкого сортування для створення робочого алгоритм у розподілу, а не створювати алгоритм розподілу з нуля[24].

Об'ємне дослідження декількох класичних експериментів на обмеженість функцією показало спільну тему подолання прототипів — ті, що успішно завершили завдання, мали здатність поглянути далі прототипу або початкового призначення предмету, який вони використовували, а ті, хто не змогли завершити завдання, не могли відкинути початкове призначення предмету. Те саме відбувалось і в дослідженнях на обмеження функцією і категоризацію. Розподіл по категоріях на перший погляд непов'язаних предметів був легший для тих, які могли поглянути далі початкової функції. Тому для уникнення обмеженості функцією необхідно подолати прототип. Карневейл у статті 1998 року[25] пропонує аналізувати об'єкт та подумки поділяти його на компоненти і вивчати можливі функції таких компонентів. При цьому людина може ознайомитись з новими способами використання предметів, наданих їм для вирішення завдання. Людина починає думати більш креативно та долає прототипи, які обмежують її здатність успішно вирішити завдання на обмеженість функцією.[25]

Для кожного об'єкту слід відділити його функцію від форми. Маккафрі у статті 2012 року[26] описує ефективну техніку для такої дії — об'єкт слід ділити на частини і при цьому задавати собі два питання: «Чи можу я ще далі поділити цю частину?» Якщо так — ділити. «Чи мій поточний опис об'єкту містить його використання?» Якщо так — створити більш загальний опис, що включає його форму та матеріал.