Петерсонове сімейство

Петерсонове сімейство в теорії графів є множиною з семи графів без орієнтації, яка включає в себе граф Петерсена та повний граф K6. Петерсонове сімейство названо на честь датского математика Юліуса Петерсена.

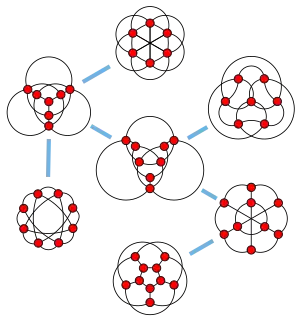
Петерсонове сімейство. Повний граф K6 вгорі, граф Петерсена внизу. Блакитні риски відповідають Δ-Y або Y-Δ перетворенням між графами сімейства.

Будь-який граф сімейства може бути перетворений на будь-який інший граф у сімействі Y-Δ перетворенням, яке замінює трикутник на вершину степіня три або навпаки (див. рисунок). Ці сім графів утворюють заборонені підграфи для незачепленого вкладення графів, тобто такі графи, які можуть бути вбудовані в тривимірний простір так, щоб не було двох зчеплених циклів у графі.[1] Робертсон та ін. вирішили питання Сакса, показавши, що графи, вкладені без зачеплень — це в точності ті графи, які не мають членів петерсенова сімейства як міноров.[2] Вони також є одними з заборонених підграфів для YΔY-редукованих графів.[3][4]


Примітки
  1. Robertson, Neil; Seymour, P. D.; Thomas, Robin (1993). Linkless embeddings of graphs in 3-space. Bulletin of the American Mathematical Society 28 (1): 84–89. MR 1164063. arXiv:math/9301216. doi:10.1090/S0273-0979-1993-00335-5..
  2. Sachs, Horst (1983). On a spatial analogue of Kuratowski's Theorem on planar graphs – an open problem. У Horowiecki, M.; Kennedy, J. W.; Sysło, M. M. Graph Theory: Proceedings of a Conference held in Łagów, Poland, February 10–13, 1981. Lecture Notes in Mathematics 1018. Springer-Verlag. с. 230–241. doi:10.1007/BFb0071633..
  3. Truemper, Klaus (1992). Matroid Decomposition. Academic Press. с. 100–101..
  4. Yu, Yaming (2006). More forbidden minors for wye-delta-wye reducibility. Electronic Journal of Combinatorics 13 (1): #R7..
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.