Простий вузол (теорія вузлів)
В теорії вузлів простий вузол або просте зачеплення — вузол, який, у певному сенсі, нерозкладний. Точніше, це нетривіальний вузол, який не можна подати у вигляді конкатенації двох нетривіальних вузлів. Про вузли, які не є простими, кажуть як про складені вузли або складені зачеплення. Визначити, чи є даний вузол простим чи ні, може виявитися складною задачею.
Приклади
Хорошим прикладом сімейства простих вузлів служать торичні вузли. Ці вузли утворюються шляхом накручування кола на тор p разів в одному напрямку і q разів в іншому, де p і q є взаємно простими цілими числами.
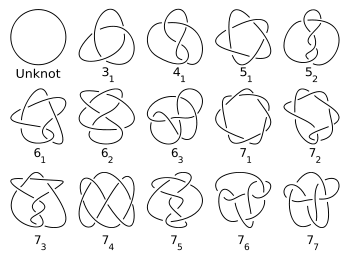
Найпростіший простий вузол — це трилисник з трьома перетинами. Трилисник є, фактично, (2, 3)-торичним вузлом. Вузол «вісімка» з чотирма перетинами є найпростішим неторичним вузлом. Для будь-якого додатного цілого числа n є скінченне число простих вузлів з n перетинами. Перші кілька значень числа простих вузлів (послідовність A002863 з Онлайн енциклопедії послідовностей цілих чисел, OEIS) подані в таблиці.
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| Число простих вузлів з n перетинами |
0 | 0 | 1 | 1 | 2 | 3 | 7 | 21 | 49 | 165 | 552 | 2176 | 9988 | 46 972 | 253 293 | 1 388 705 |
| Складені вузли | 0 | 0 | 0 | 0 | 0 | 2 | 1 | 4 | … | … | … | … | ||||
| Всього | 0 | 0 | 1 | 1 | 2 | 5 | 8 | 25 | … | … | … | … |
Зауважимо, що антиподи враховувалися в цій таблиці і на малюнку нижче тільки один раз (тобто вузол і його дзеркальне відображення вважаються еквівалентними).
Теорема Шуберта
Теорема, що належить Хорсту Шуберту, стверджує, що будь-який вузол можна єдиним чином подати у вигляді конкатенації простих вузлів[1].
Див. також
- Список простих вузлів
Примітки
- Schubert, 1949, с. 57—104.
Література
- H. Schubert. Die eindeutige Zerlegbarkeit eines Knotens in Primknoten // S.-B Heidelberger Akad. Wiss. Math.-Nat. Kl. — 1949.
Посилання
- Weisstein, Eric W. Prime Knot(англ.) на сайті Wolfram MathWorld.
- [Prime Links with a Non-Prime Component] Атлас вузлів (англ.)