Прохідний пішак
В шахах прохідний пішак це пішак навпроти якого нема пішаків суперника, які б завадили просунути його на 8-му (для білих), або 1-шу (для чорних) горизонталь. Тобто нема пішаків суперника попереду на тій самій та (або) суміжній вертикалі. Прохідні пішаки можуть бути перевагою, оскільки лише фігури суперника можуть завадити їх проходу на останню горизонталь, а отже їх заміні на фігуру.
| a | b | c | d | e | f | g | h | ||
| 8 |  | 8 | |||||||
| 7 | 7 | ||||||||
| 6 | 6 | ||||||||
| 5 | 5 | ||||||||
| 4 | 4 | ||||||||
| 3 | 3 | ||||||||
| 2 | 2 | ||||||||
| 1 | 1 | ||||||||
| a | b | c | d | e | f | g | h | ||
На діаграмі справа, білі пішаки на b5, c4, та e5 є прохідними. Чорний пішак на d4 є прохідним. Якщо чорні зіграють fxg4, тоді вони також будуть мати прохідного пішака на g4, а у білих утвориться прохідний пішак на f4.
Захищений прохідний пішак
| a | b | c | d | e | f | g | h | ||
| 8 |  | 8 | |||||||
| 7 | 7 | ||||||||
| 6 | 6 | ||||||||
| 5 | 5 | ||||||||
| 4 | 4 | ||||||||
| 3 | 3 | ||||||||
| 2 | 2 | ||||||||
| 1 | 1 | ||||||||
| a | b | c | d | e | f | g | h | ||
Прохідний пішак, що захищений своїми власними пішаками, має назву захищений прохідний пішак. На першій діаграмі цієї статті, пішаки на вертикалях b та e є захищеними. Два чи більше пішаків на суміжних вертикалях називаються пов'язаними прохідними пішаками (див. пов'язані пішаки), і вони дуже сильні. На верхній діаграмі білі пішаки b та c є пов'язаними. Часто стратегічно вигідно для гравця з пов'язаними пішаками ставити їх на суміжні вертикалі і просувати в сполуці, тому що в цьому випадку складніше їх заблокувати.
Буває, що гравці жертвують легкі фігури щоб звільнити вертикаль для проходу пішака. На діаграмі справа (Михайло Ботвинник–Хосе Рауль Капабланка), для того щоб скористатись прохідним пішаком на е6 і зняти його блокаду ферзем, білі продовжили 30. Ba3! Qxa3 31. Nh5+! gxh5 32. Qg5+ Kf8 33. Qxf6+, гарантувавши прохід пішака е . У цьому випадку жертва слона та коня варта того, бо це усуває ферзя та коня чорних зі шляху. Тепер шлях пішака є вільним для проходу на 8-у горизонталь, а пішаки чорних не в змозі завадити проходу.[1]
Крайній прохідний пішак
| a | b | c | d | e | f | g | h | ||
| 8 |  | 8 | |||||||
| 7 | 7 | ||||||||
| 6 | 6 | ||||||||
| 5 | 5 | ||||||||
| 4 | 4 | ||||||||
| 3 | 3 | ||||||||
| 2 | 2 | ||||||||
| 1 | 1 | ||||||||
| a | b | c | d | e | f | g | h | ||
Крайній прохідний пішак це пішак, що знаходиться скраю шахівниці, або поблизу від нього, і відділений певною кількістю вертикалей від короля суперника. Наявність такого пішака часто призводить до значної переваги одного з гравців, бо король суперника не встигає одночасно проконтролювати обидва краї дошки.
В позиції на діаграмі справа з кандидатського матчу 1971 між Боббі Фішером та Бентом Ларсеном,[2] завдяки крайньому прохідному пішаку на вертикалі а білі володіють виграшною перевагою, навіть попри матеріальну рівновагу. Цей пішак примушую короля чорних залишатись поблизу щоб затримати його, тоді як король білих може спокійно побити пішаки на іншому фланзі. Білі виграють таким чином:
- 41. Kd4 Kd6
- 42. a5 f6
- 43. a6 Kc6
- 44. a7 Kb7
- 45. Kd5 h4
- If 45...f5 46. h4 виграє.
- 46. Ke6 1–0 [3].
| a | b | c | d | e | f | g | h | ||
| 8 |  | 8 | |||||||
| 7 | 7 | ||||||||
| 6 | 6 | ||||||||
| 5 | 5 | ||||||||
| 4 | 4 | ||||||||
| 3 | 3 | ||||||||
| 2 | 2 | ||||||||
| 1 | 1 | ||||||||
| a | b | c | d | e | f | g | h | ||
Крайній прохідний пішак є дуже потужним в ендшпілі з легкими фігурами. Він не такий потужний в ендшпілі з турами, якщо тура протилежного кольору може стати позаду нього (діаграми), див. Правило Тарраша [4], [5].
Прохідні пішаки в ендшпілі
| a | b | c | d | e | f | g | h | ||
| 8 |  | 8 | |||||||
| 7 | 7 | ||||||||
| 6 | 6 | ||||||||
| 5 | 5 | ||||||||
| 4 | 4 | ||||||||
| 3 | 3 | ||||||||
| 2 | 2 | ||||||||
| 1 | 1 | ||||||||
| a | b | c | d | e | f | g | h | ||
| a | b | c | d | e | f | g | h | ||
| 8 |  | 8 | |||||||
| 7 | 7 | ||||||||
| 6 | 6 | ||||||||
| 5 | 5 | ||||||||
| 4 | 4 | ||||||||
| 3 | 3 | ||||||||
| 2 | 2 | ||||||||
| 1 | 1 | ||||||||
| a | b | c | d | e | f | g | h | ||
Прохідні пішаки часто мають вирішальне значення в ендшпілі. Позиція зліва є яскравим прикладом цього. Здається що білі в безнадійному становищі оскільки чорний король скоро атакує пішаки ...Kg4. Насправді ж, білі за допомогою комбінації з жертвою створюють прохідного пішака і виграють: 1. g6! fxg6 (або 1...hxg6 2.f6! gxf6 3.h6!) 2. h6! gxh6 3. f6! і тільки що створений прохідний пішак білих дає їм перемогу. Якщо ж хід чорних, то вони повинні уникнути цієї комбінації граючи 1... g6! (не 1...f6 2.h6!, не 1...h6 2.f6!).
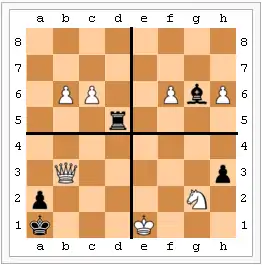
Оскільки прохідні пішаки часто не мають пішаків навпроти них, які б їх зупинили, загроза перетворення часто змушує суперника заблокувати їх або побити. А це є втратою часу і робить фігури нерухомими. Зрештою, цінність віддаленого прохідного пішака часом є рівною, або навіть більшою ніж фігури. На діаграмі справа можна побачити чотири приклади цього. В лівому верхньому чотирикутнику шахівниці пов'язані прохідні пішаки білих на шостій горизонталі є сильнішими за чорну туру. Навіть якщо хід чорних, вони не можуть зупинити одного з пішаків від перетворення. Аналогічно, у верхньому правому чотирикутнику чорний слон не може зупинити обох пішаків. Білий пішак проходить після 1. f7 (1.h7 також працює) Bxf7 2. h7 після чого 3. h8=Q. В лівому нижньому чотирикутнику, білий ферзь не може зупинити прохід чорного пішака без пата. Нижній правий чотирикутник показує незграбність коня проти прохідного пішака, особливо крайнього. В даному випадку наявність білого коня навіть заважає. Якщо білий король ходить 1. Kf2 сподіваючись на 1...hxg2? 2.Kxg2), чорні грають 1... h2! і 2... h1=Q.
| a | b | c | d | e | f | g | h | ||
| 8 |  | 8 | |||||||
| 7 | 7 | ||||||||
| 6 | 6 | ||||||||
| 5 | 5 | ||||||||
| 4 | 4 | ||||||||
| 3 | 3 | ||||||||
| 2 | 2 | ||||||||
| 1 | 1 | ||||||||
| a | b | c | d | e | f | g | h | ||
Разючий (і дуже незвичний) приклад сили прохідних пішаків можна побачити на діаграмі зліва, завершення етюда Леопольда Митрофанова. Чорні, з ферзем, слоном, і конем, не можуть нічого вдіяти з двома прохідними пішаками білих, з подвійною загрозою 10.b7# і 10.c8=Q+ Bb8 11.b7#.
Див. також
- Пов'язані пішаки
- Подвоєні пішаки
- Ізольований пішак
- Пішакова структура
- Правило Тарраша
Примітки
- http://www.chessgames.com/perl/chessgame?gid=1031957 Botvinnik–Capablanca
- http://www.chessgames.com/perl/chessgame?gid=1044348 Fischer–Larsen
- Müller, Karsten; Pajeken, Wolfgang
- Müller, Karsten; Pajeken, Wolfgang pp.40-41
- Levenfish, Grigory; Smyslov, Vasily p=157
Посилання
- Golombek, Harry (1977), Golombek's Encyclopedia of Chess, Crown Publishing, ISBN 0-517-53146-1
- Hooper, David; Whyld, Kenneth (1992), The Oxford Companion to Chess (second вид.), Oxford University Press, ISBN 0-19-866164-9
- Levenfish, Grigory; Smyslov, Vasily (1971), Rook endings, Batsford, ISBN 0-7134-0449-3
- Müller, Karsten; Pajeken, Wolfgang (2008), How to Play Chess Endings, Gambit Publications, ISBN 978-1-904600-86-2