Сортування Шелла

Сортування Шелла
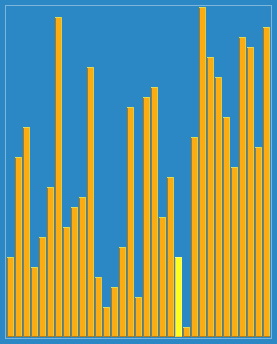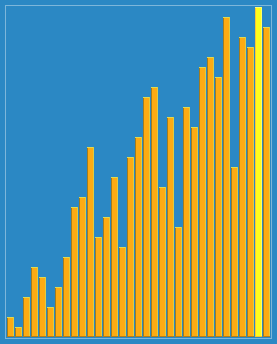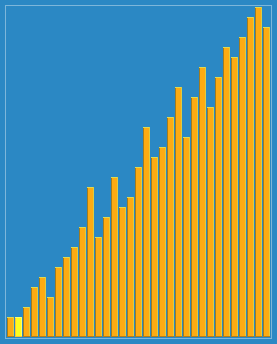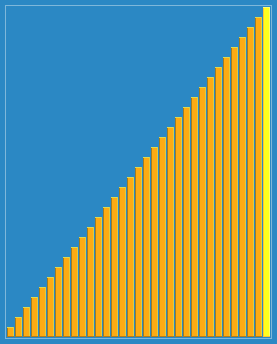	; Демонстрація сортування Шелла з інтервалами 23, 10, 4, 1.
Клас	Алгоритм сортування
Структура даних	масив
Найгірша швидкодія
Оптимальний	Переважно ні

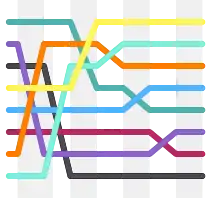
Сортува́ння Ше́лла — це алгоритм сортування, що є узагальненням сортування включенням.

Сортування Шелла колір алгоритм бари

Алгоритм базується на двох тезах:

Сортування включенням ефективне для майже впорядкованих масивів.
Сортування включенням неефективне, тому що переміщує елемент тільки на одну позицію за раз.

Тому сортування Шелла виконує декілька впорядкувань включенням, кожен раз порівнюючи і переставляючи елементи, що розташовані на різній відстані один від одного.

Сортування Шелла не є стабільним.

Історія

Сортування Шелла названо на честь автора — Дональда Шелла, який опублікував цей алгоритм у 1959[1] році. В деяких пізніших друкованих виданнях алгоритм називають сортуванням Шелла-Мацнера, за ім'ям Нортона Мацнера. Але сам Мацнер стверджував: «Мені не довелось нічого робити з цим алгоритмом, і моє ім'я не має пов'язуватись з ним».[2]

Ідея алгоритму

На початку обираються m-елементів: $d_{1},d_{2},\dots ,d_{m}$ , причому, $d_{1}>d_{2}>\dots >d_{m}=1$ .

Потім виконується m впорядкувань методом включення, спочатку для елементів, що стоять через $\;d_{1}$ , потім для елементів через $\;d_{2}$ і т. д. до $\;d_{m}=1$ .

Ефективність досягається тим, що кожне наступне впорядкування вимагає меншої кількості перестановок, оскільки деякі елементи вже стали на свої місця.

Псевдокод

Сам алгоритм не залежить від вибору m і d, тому будемо вважати, що вони задані.

 $Shell\_Sort(A,N)\;$ 
1. for  $k\leftarrow 1$  to  $\;m$ 
2. do for  $i\leftarrow d[k]+1$  to  $\;N$ 
3.    do  $a\leftarrow A[i]$ 
4.        $j\leftarrow i$ 
5.       while  $\;j-d[k]\geq 1$  і  $\;A[j-d[k]]>a$ 
6.       do  $A[j]\leftarrow A[j-d[k]]$ 
7.           $j\leftarrow j-d[k]$ 
8.        $A[j]\leftarrow a$

Коректність алгоритму

Оскільки $\;d_{m}=1$ то на останньому кроці виконується звичайне впорядкування включенням всього масиву, а отже кінцевий масив буде впорядкованим.

Час роботи

Час роботи залежить від вибору значень елементів масиву d. Існує декілька підходів вибору цих значень:

При виборі $d_{1}=\left\lfloor {\frac {N}{2}}\right\rfloor ,d_{2}=\left\lfloor {\frac {d_{1}}{2}}\right\rfloor ,d_{3}=\left\lfloor {\frac {d_{2}}{2}}\right\rfloor ,\dots ,d_{m}=1$ час роботи алгоритму, в найгіршому випадку, є $\;O(N^{2})$ .
Якщо d — впорядкований за спаданням набір чисел виду ${\frac {3^{j}-1}{2}},j\in \mathbb {N} ,d_{i}<N$ , то час роботи є $\;O\left(N^{\frac {3}{2}}\right)$ .
Якщо d — впорядкований за спаданням набір чисел виду $2^{i}3^{j},i,j\in \mathbb {N} ,d_{k}<N$ , то час роботи є $\;O(N\log ^{2}N)$ .
Якщо d — впорядкований за спаданням набір чисел одного з видів:
- $4^{k}+3\cdot 2^{k-1}+1,k\in \mathbb {N}$ (з додатковим членом 1 на початку)
- або ${\begin{cases}9\left(2^{k}-2^{\frac {k}{2}}\right)+1&k{\text{ even}},\\8\cdot 2^{k}-6\cdot 2^{(k+1)/2}+1&k{\text{ odd}}\end{cases}}$ ,

то час роботи алгоритму становить $O\left(N^{\frac {4}{3}}\right)$ (Sedgewick, 1986[3]).

Існують інші, оптимальніші послідовності, для яких не визначена верхня асимптотична оцінка, наприклад:
- послідовність A102549 є найефективнішою з відомих, хоча формула для її визначення невідома (Ciura, 2001[4]);
- послідовність A108870 є найшвидшою з тих, що мають відому формулу: $\left\lceil {\frac {1}{5}}\left(9\cdot \left({\frac {9}{4}}\right)^{k-1}-4\right)\right\rceil$ (Tokuda, 1992[5]).

Приклад роботи

Проілюструймо роботу алгоритму на вхідному масиві A = (5,16,1,32,44,3,16,7), d = (5,3,1).

Масив після впорядкування з кроком в 5: (3,16,1,32,44,5,16,7) — зроблено 1 обмін.
Масив після впорядкування з кроком 3: (3,7,1,16,16,5,32,44) — зроблено 3 обміни.
Масив після впорядкування з кроком 1: (1,3,5,7,16,16,32,44) — зроблено 5 обмінів.

Отже, весь масив впорядковано за 9 операцій обміну.

Реалізація (Паскаль/DELPHI)

PROGRAM MyVerShellSort;
{$APPTYPE CONSOLE}
USES SysUtils;
TYPE massive=array[1..100] of integer;
VAR A:massive; n:integer;
procedure RndArrInput(var a1:massive; n1:integer);
  var i1:integer;
  begin
    randomize;
    for i1:=1 to n1 do
      a1[i1]:=10-random(20);
  end;
procedure Arroutput(a2:massive; n2:integer);
  var i2:integer;
  begin
    for i2:=1 to n2 do
      write(a2[i2],' ');
  end;
procedure change (var k,l:integer);
  var tmp:integer;
  begin
    tmp:=k; k:=l; l:=tmp;
  end;
procedure  ShellSort(var  A:massive;  N:integer);
  var  i,j,h:integer;
  begin
    h:=N  div  2;
    while  h>0  do
      begin
        for  i:=1  to  N-h  do
          begin
            j:=i;
            while  (j>=1)and(A[j]>A[j+h])  do
              begin
                change(a[j],a[j+h]);
                dec(j);
              end;
          end;
        h:=h  div  2;
      end;
  end;
BEGIN
writeln('enter data:');
readln(n);
RndArrInput(a,n);
ArrOutPut(a,n); readln;
ShellSort(a,n);
ArrOutPut(a,n);
readln;
END.

Реалізація на C / C++

void sort_shell(int *a, int N)
{
    for (int d = N/2; d >= 1; d /= 2)
        for (int i = d; i < N; i++)
            for (int j = i; j >= d && a[j-d] > a[j]; j -= d)
                swap(a[j], a[j-d]);
}

Примітки

Shell, D.L. (1959). A high-speed sorting procedure. Communications of the ACM 2 (7): 30–32. doi:10.1145/368370.368387.
Shell sort. National Institute of Standards and Technology. Архів оригіналу за 26 червня 2013. Процитовано 17 липня 2007.
Sedgewick, Robert (1986). A New Upper Bound for Shellsort. Journal of Algorithms 7 (2): 159–173. doi:10.1016/0196-6774(86)90001-5.
Ciura, Marcin (2001). Best Increments for the Average Case of Shellsort. У Freiwalds, Rusins. Proceedings of the 13th International Symposium on Fundamentals of Computation Theory. London: Springer-Verlag. с. 106–117. ISBN 3-540-42487-3.
Tokuda, Naoyuki (1992). An Improved Shellsort. У van Leeuven, Jan. Proceedings of the IFIP 12th World Computer Congress on Algorithms, Software, Architecture. Amsterdam: North-Holland Publishing Co. с. 449–457. ISBN 0-444-89747-X.

Посилання

Наочна демонстрація сортування Шелла угорськими танцюристами.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Shell, D.L. (1959). A high-speed sorting procedure. Communications of the ACM 2 (7): 30–32. doi:10.1145/368370.368387.

[2] Shell sort. National Institute of Standards and Technology. Архів оригіналу за 26 червня 2013. Процитовано 17 липня 2007.

[Sedgewick2-3] Sedgewick, Robert (1986). A New Upper Bound for Shellsort. Journal of Algorithms 7 (2): 159–173. doi:10.1016/0196-6774(86)90001-5.

[:0-4] Ciura, Marcin (2001). Best Increments for the Average Case of Shellsort. У Freiwalds, Rusins. Proceedings of the 13th International Symposium on Fundamentals of Computation Theory. London: Springer-Verlag. с. 106–117. ISBN 3-540-42487-3.

[5] Tokuda, Naoyuki (1992). An Improved Shellsort. У van Leeuven, Jan. Proceedings of the IFIP 12th World Computer Congress on Algorithms, Software, Architecture. Amsterdam: North-Holland Publishing Co. с. 449–457. ISBN 0-444-89747-X.