Список з пропусками

Список з пропусками
Тип	Список
Винайдено	1989
Винайшли	Вільям П'ю
Обчислювальна складність; у записі великого О

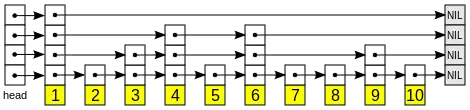
В інформатиці, список з пропусками (англ. skip list) — структура даних, яка дозволяє швидкий пошук в упорядкованій послідовності елементів. Швидкий пошук стає можливим через утримання зв'язаної ієрархії підпослідовностей, кожна з яких пропускає кілька елементів з попереднього списку. Пошук стартує в найрозрідженішому списку, і триває допоки не знайдені два послідовних елементи один менший і один більший від шуканого елементу. Через ієрархічні зв'язки ці два елементи зв'язані з елементами наступного по щільності списку, в якому пошук продовжується. Таким чином ми доходимо до повного списку, без пропусків. Елементи пропущені у розріджених списках можуть обиратись імовірнісно.[2][3]

Опис

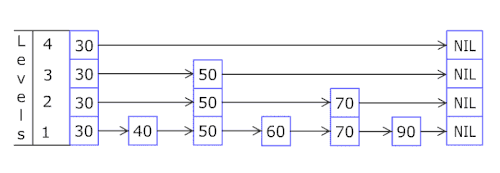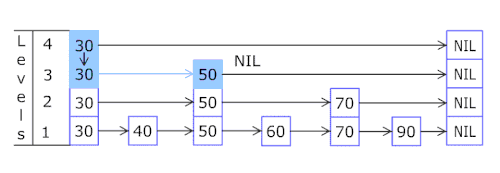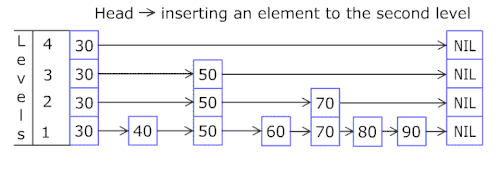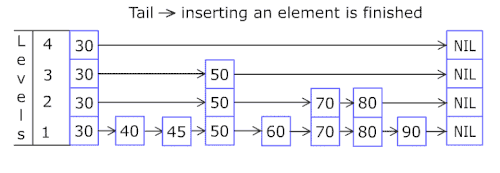
Список з пропусками будується пошарово. Нижній шар це звичайний впорядкований зв'язаний список. Кожен наступний шар поводиться як «експрес-лінія» для нижнього списку, де елементи з шару $i$ з'являються в шарі $i+1$ з певною ймовірністю $p$ (найуживанішими значеннями для $p$ є $1/2$ і $1/4$ ). В середньому, кожний елемент з'являється в $1/(1-p)$ списках, найвищий елемент (зазвичай особливий елемент на початку списку з пропусками) в $\log _{1/p}n\,$ списках.

Пошук цільового елементу починається з головного елемента верхнього списку, і продовжується горизонтально доки поточний елемент є більшим або рівним цільовому. Якщо поточний елемент дорівнює цільовому, пошук завершується. якщо поточний елемент більший ніж цільовий або пошук досяг кінця списку зв'язного списку, процедуру повторюють після повернення до попереднього елемента і спуску на один рівень нижче. Сподіване число кроків в кожному зв'язаному списку становить не більше ніж $1/p.$ Вибір різних значень для $p$ дає можливість досягти необхідного балансу між швидкість пошуку і місцем на диску.

Вставляння елемента у список з пропусками

Аналіз вартості пошуку

З високою імовірністю[4], кожен пошук у списку з пропусками коштує $O(\lg {n}).$

Лема

З високою імовірністю, список з пропусками з $n$ елементами має $O(\lg {n})$ рівнів.

Доведення:

$Pr\{$ елемент $x$ досяг вищого рівня ніж $c\lg {n}\}=1/p^{c\lg _{p}{n}}=1/n^{c}$
Застосовуючи нерівність Буля для імовірності об'єднання подій:
$Pr\{$ будь-який елемент досяг вищого рівня ніж $c\lg {n}\}\leq \sum _{1}^{n}1/n^{c}=1/n^{c-1}$
Отже, імовірність помилки[4] поліноміально мала і експоненту $\alpha =c-1$ можна зробити як завгодно великою через відповідний вибір сталої в $O(\lg {n}).$

Доведення теореми (нарис)

Ідея: Аналізувати пошук у зворотньому напрямку — від листа до кореня
- Пошук починається з елемента найнижчого рівня
- На кожному відвіданому вузлі:
  - Якщо вершина не підвищували до наступного рівня, тоді ми рухаємось (прийшли) ліворуч
  - Якщо вершина підвищували до наступного рівня, тоді ми рухаємось (прийшли) вгору
- Пошук завершується в корені
Відомо, що висота становить $O(\lg {n})$ з високою імовірністю, наприклад $c\lg {n}$
Отже, кількість рухів догори є щонайбільше $c\lg {n}$ , з високою імовірністю
Звідси, вартість пошуку є кількістю подій необхідних, щоб досягнути рівня $c\lg {n}$ $\text{[math]}$ (якщо $p=1/2$ $\text{[math]}$ тоді скільки підкидань монети потрібно, щоб отримати $c\lg {n}$ $\text{[math]}$ аверсів)
- Інтуїтивно, $O(\lg {n})$

Примітки

http://www.cs.uwaterloo.ca/research/tr/1993/28/root2side.pdf
П'ю, Вільям (червень 1990). Skip lists: a probabilistic alternative to balanced trees. Communications of the ACM (ACM) 33 (6): 668–676. doi:10.1145/78973.78977. Процитовано 15.11.2014.
Детерміністичні списки з пропусками (англ.)
Параметризована подія $E_{\alpha }$ відбувається з високою імовірністю якщо, для будь-якого $\alpha \geq 1,E_{\alpha }$ відбувається з імовірністю не менше ніж $1=c_{\alpha }/n^{\alpha },$ де $c_{\alpha }$ є сталою залежною тільки від $\alpha .$ Терм $c_{\alpha }/n^{\alpha }$ називається імовірністю помилки.

Див. також

Фільтр Блума

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[cs.uwaterloo-1] ttp://www.cs.uwaterloo.ca/research/tr/1993/28/root2side.pdf

[pugh-2] П'ю, Вільям (червень 1990). Skip lists: a probabilistic alternative to balanced trees. Communications of the ACM (ACM) 33 (6): 668–676. doi:10.1145/78973.78977. Процитовано 15.11.2014.

[3] Детерміністичні списки з пропусками (англ.)

[whp-4] Параметризована подія $E_{\alpha }$ відбувається з високою імовірністю якщо, для будь-якого $\alpha \geq 1,E_{\alpha }$ відбувається з імовірністю не менше ніж $1=c_{\alpha }/n^{\alpha },$ де $c_{\alpha }$ є сталою залежною тільки від $\alpha .$ Терм $c_{\alpha }/n^{\alpha }$ називається імовірністю помилки.

Список з пропусками
Тип	Список
Винайдено	1989
Винайшли	Вільям П'ю
Обчислювальна складність у записі великого О
	Середня	Найгірша
Простір	O(n)	O(n log n)[1]
Пошук	O(log n)	O(n)[1]
Вставляння	O(log n)	O(n)
Видалення	O(log n)	O(n)