Нотація Ландау

«О» велике. Нехай задані дві комплекснозначні функції ${\displaystyle f(z)}$ та ${\displaystyle g(z)}$ визначені в деякій множині ${\displaystyle D}$ комплексної площини. Тоді говорять, що

якщо існує константа K >0, що виконується нерівність |f(z)| ≤ K |g(z)| для ${\displaystyle z\in D}$.

«O» велике в околі ${\displaystyle z_{0}}$. Нехай ${\displaystyle f(z)}$ і ${\displaystyle g(z)}$ дві комплекснозначні функції визначені в деякій множині ${\displaystyle D}$ комплексної площини, замикання якої містить точку ${\displaystyle z_{0}}$ (тобто, ${\displaystyle z_{0}}$ є граничною точкою ${\displaystyle D}$). Тоді ми пишемо

${\displaystyle f(z)=O(g(z))}$ при ${\displaystyle z\to z_{0}}$ з ${\displaystyle D}$

якщо існує число ${\displaystyle \delta >0}$ таке, що

${\displaystyle f(z)=O(g(z)),\ z\in D,\ 0<|z-z_{0}|<\delta }$

у сенсі означення «О» великого. Тобто, ${\displaystyle f}$ обмежена величиною добутку константи на ${\displaystyle g}$ для всіх ${\displaystyle z}$ з ${\displaystyle D}$, які лежать досить близько до ${\displaystyle z_{0}}$.

«O» велике в нескінченності. Нехай ${\displaystyle f(z)}$ і ${\displaystyle g(z)}$ дві комплекснозначні функції визначені в необмеженій множині ${\displaystyle D}$ комплексної площини. Тоді ми кажемо, що

${\displaystyle f(z)=O(g(z))}$ при ${\displaystyle z\to \infty }$ з ${\displaystyle D}$

якщо існує число ${\displaystyle M>0}$ так що

${\displaystyle f(z)=O(g(z)),\ z\in D,\ |z|<M}$,

у сенсі означення «О» великого. Тобто, ${\displaystyle f}$ обмежена величиною добутку деякої константи на ${\displaystyle g}$, для достатньо великих ${\displaystyle z}$ з ${\displaystyle D}$.

«o» маленьке. Нехай ${\displaystyle f(z)}$ і ${\displaystyle g(z)}$ дві комплекснозначні функції визначені в деякій множині ${\displaystyle D}$ комплексної площини замикання якої містить точку ${\displaystyle z_{0}}$. Тоді ми кажемо, що

${\displaystyle f(z)=o(g(z))}$ при ${\displaystyle z\to z_{0}}$ з ${\displaystyle D}$

якщо для довільного ${\displaystyle \varepsilon >0}$, як завгодно малого, існує відповідне йому ${\displaystyle \delta (\varepsilon )>0}$, що

${\displaystyle |f(z)|\leqslant \varepsilon |g(z)|}$ для ${\displaystyle z\in D}$ і ${\displaystyle 0<|z-z_{0}|<\delta (\varepsilon )}$.

Тобто, ${\displaystyle f}$ є меншим за величиною за будь-який малий добуток ${\displaystyle g}$ для ${\displaystyle z\in D}$ досить близьких до точки ${\displaystyle z_{0}}$.

«о» маленьке в нескінченності Нехай ${\displaystyle f(z)}$ і ${\displaystyle g(z)}$ комплекснозначні функції визначені в необмеженій множині ${\displaystyle D}$ комплексної площини. Тоді ми пишемо

${\displaystyle f(z)=o(g(z))}$ при ${\displaystyle z\to \infty }$ з ${\displaystyle D}$

якщо для довільного ${\displaystyle \varepsilon >0}$, як завгодно малого, ми можемо знайти відповідне ${\displaystyle M(\varepsilon )>0}$ таке що

Функції f(x) та g(x) називають функціями одного порядку, якщо f(x) = O(g(x)) та g(x) є O(f(x)) для x ${\displaystyle \to }$ x₀;

Часто для позначення того, що f(x) є O(g(x)) використовується запис f(x) = O(g(x)), хоч це не зовсім правильно і в деяких випадках може привести до плутанини.

Нехай ${\displaystyle n}$ і ${\displaystyle m}$ цілі числа. Якщо ${\displaystyle n\geq m}$, то ${\displaystyle z^{m}=O(z^{n})}$ при ${\displaystyle z\to \infty }$. Для доведення цього запишемо

Покладемо ${\displaystyle M=10}$. Тоді ${\displaystyle |z|>M}$ означає що ${\displaystyle |z|^{m-n}\leq 10^{m-n}}$, оскільки ${\displaystyle n\geq m}$. Отже, якщо ${\displaystyle |z|>10}$, нерівність ${\displaystyle |z|^{m}\leq K|z^{m-n}|}$ виконується при виборі ${\displaystyle K=10^{m-n}}$. Також, з аналогічним обмеженням на ${\displaystyle n}$ та ${\displaystyle m}$, ми маємо, що ${\displaystyle z^{n}=O(z^{m})}$ при ${\displaystyle z\to 0}$ з ${\displaystyle \mathbb {C} }$. Для доведення цього запишемо

Виберемо, наприклад, ${\displaystyle \delta =3}$. Тоді, ${\displaystyle 0<|z|<3}$ означає, що ${\displaystyle |z|^{n-m}<3^{n-m}}$ оскільки ${\displaystyle n\geq m}$.

Графіки деяких поширених функцій.

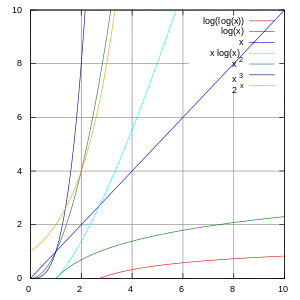
Нижче наведений список класів функцій, які часто зустрічаються в аналізі алгоритмів. Тут n ${\displaystyle \to }$ ∞, с — константа. Функції, які зростають повільніше, наведені першими.

• Таблиця математичних символів