Співвідношення Фабер — Джексона
Співвідношення Фабер — Джексона — рання емпірична залежність між світністю та шириною спектральних ліній для еліптичних галактик, яку виявили астрономи Сандра М. Фабер і Роберт Ерл Джексон 1976 р.[1]
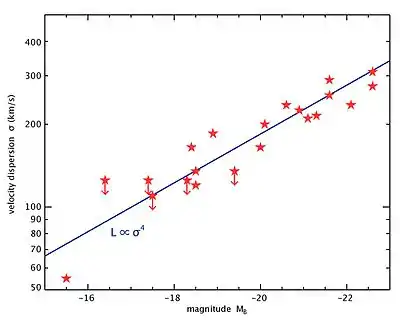
Співвідношення Фабер — Джексона показано прямою лінією.
Оскільки ширина спектральних ліній галактики фактично визначається дисперсією швидкості зір, то по суті, співвідношення Фабер — Джексона є залежністю між дисперсією швидкості зір та світністю галактики. Ця залежність має вигляд[2]:
де:
- LB — світність галактики у фільтрі B;
- σ — дисперсія швидкості зір;
- γ — індекс, який приблизно дорівнює 4 (точно визначається зі спостережень).
Надійне калібрування залежності виконати не вдалося, оскільки відстані до галактик, за якими будувалося співвідношення, були відомі зі значною похибкою. Як було встановлено пізніше, величина індексу залежить від діапазону світності галактики.
Зараз співвідношення Фабер—Джексона інтерпретується як проекція фундаментальних площин еліптичних галактик. Одне з основних застосувань цього співвідношення — визначення відстані до галактик[джерело?].
Теорія
Гравітаційний потенціал масового розподілу радіусу і маси задається виразом:
Де α є сталою що залежить, наприклад, від профілю густини системи і G гравітаційна стала. Для сталої густини
Кінетична енергія дорівнює (нагадаємо, що це одновимірна дисперсія швидкостей. Тому ).
З теореми віріалу () випливає, що
Якщо припустити, що відношення маси до світності, , є сталою величиною, тобто , ми можемо використати цей та попередній вирази, щоб отримати співвідношення між та :
Ввівши поверхневу яскравість як , та припустивши, що вона є сталою (що суто з теоретичної точки зору є необґрунтованим припущенням) ми отримаємо
Використовуючи цю формулу і об'єднавши її з співвідношенням між і , в результаті отримаємо
і переписавши наведений вище вираз, ми, нарешті, отримаємо співвідношення між світністю і дисперсією швидкості:
тобто
Враховуючи той факт, що масивні галактики утворюються внаслідок гомологічного злиття, а тьмяніші — шляхом дисипації, припущення про постійну яскравість поверхні більше не може бути використаним. Емпірично, яскравість поверхні, має пік приблизно . Тоді попереднє співвідношення перетворюється на
Для менш масивних галактик, і
для більш масивних. Із цієї уточненої формули випливає, що фундаментальна площина розділяється на дві площини нахилені приблизно на 11 градусів одна до одної.
Але навіть найперші галактичні скупчення не мають постійної поверхневої яскравості. Аргументи на користь постійної поверхневої яскравості були вперше висунуті астрономом Еланом Р. Сендиджом 1972 року на основі трьох логічних тверджень і його власних емпіричних даних. 1975 року Дональд Ґудехус показав, що кожен з логічних аргументів був невірним і що для головних скупчень галактик спостерігалося стандартне відхилення близько на половину величини.
Оцінка відстаней до галактик
Як і співвідношення Таллі — Фішера , співвідношення Фабер — Джексона є засобом для оцінки відстані до галактик за допомогою найлегше спостережуваних властивостей галактики. При розгляді еліптичних галактик, якщо можна виміряти центральну зоряну дисперсію швидкостей, що можна здійснити порівняно легко за допомогою спектроскопії для вимірювання Доплерівського зсуву світла, випромінюваного зірками, то можна отримати оцінку справжньої світності галактики за допомогою співвідношення Фабера -Джексона. Це можна порівняти з видимою зоряною величиною галактики, яка забезпечує оцінку модуля відстані і, отже, відстані до галактики.
Об'єднавши центральну дисперсію швидкостей галактики з вимірами її центральної поверхневої яскравості і параметром радіусу, можна поліпшити оцінку відстані до галактики ще більше. Цим стандартним мірилом, або «малим галактичним радіус-параметром», , розробленим Ґудехусом 1991 року[3], може вимірювати відстані, без врахування систематичної похибки, з точністю до 31 %.
Див. також
Джерела
- The original paper by Faber & Jackson
- Фабера-Джексона співвідношення // Астрономічний енциклопедичний словник / за заг. ред. І. А. Климишина та А. О. Корсунь. — Львів : Голов. астроном. обсерваторія НАН України : Львів. нац. ун-т ім. Івана Франка, 2003. — С. 492. — ISBN 966-613-263-X.
- Gudehus's revision of the Faber–Jackson relation