Стиснений стан

Стисненим когерентним станом у квантовій механіці називають стан, у якому гайзербергова невизначеність має найменше значення. Від канонічних когерентних станів стиснені стани відрізняються тим, що невизначеність окремих змінних у парі канонічно-спряжених неоднакова. Тому в фазовому просторі такий стан зображається не колом, а стискається до еліпса, що є підставою для назви[1] [2] [3] [4] [5].

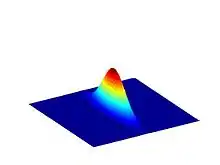
Розподіл стисненого стану в фазовому просторі амплітуда-фаза.

Для змінних положення та імпульс, наприклад, мінімальна невизначеність досягається тоді, коли

\Delta x\Delta p={\frac {\hbar }{2}},

де $\Delta x$ — невизначеність положення, $\Delta p$ — невизначеність імпульсу, а $\hbar$ — зведена стала Планка. У стисненому стані, на відміну від когерентного, $\Delta x\neq \Delta p$ , де положення та імпульс виражено в природних осциляторних одиницях.

Математичне визначення

Анімація хвильової функції амплітудно стисненого на 2 дБ когерентного стану з α=3.

Загальна хвильова функція, що задовольняє наведену рівність описується стисненим когерентним станом (систему одиниць обрано так, що $\hbar =1$ )

\psi (x)=C\,\exp \left(-{\frac {(x-x_{0})^{2}}{2w_{0}^{2}}}+ip_{0}x\right)

де $C,x_{0},w_{0},p_{0}$ — відомі сталі (стала нормування, центр хвильового пакету та математичне сподівання імпульсу). Новою рисою щодо когерентного стану є значення ширини $w_{0}$ , що є причиною, чому ці стани називаються стисненими.

Наведений стиснений стан є власним станом лінійного оператора

{\hat {x}}+i{\hat {p}}w_{0}^{2},

а відповідне власне значення дорівнює $x_{0}+ip_{0}w_{0}^{2}$ . У цьому сенсі, стан є узагальненням водночас основного та когерентного станів.

Операторне представлення

Загальна форма стисненого когерентного стану квантового оператора має вигляд

|\alpha ,\zeta \rangle =D(\alpha )S(\zeta )|0\rangle

де $|0\rangle$ — вакуумний стан, $D(\alpha )$ — оператор зміщення, а $S(\zeta )$ — оператор стиснення, що задається формулою

D(\alpha )=\exp(\alpha {\hat {a}}^{\dagger }-\alpha ^{*}{\hat {a}})

та

S(\zeta )=\exp \left({\frac {1}{2}}\left(\zeta ^{*}{\hat {a}}^{2}-\zeta {\hat {a}}^{\dagger 2}\right)\right)

де ${\hat {a}}$ та ${\hat {a}}^{\dagger }$ — оператори знищення та народження, відповідно. Для квантового гармонічного осцилятора з кутовою частотою $\omega$ , ці оператори задаються як

{\hat {a}}^{\dagger }={\sqrt {\frac {m\omega }{2\hbar }}}\left(x-{\frac {ip}{m\omega }}\right)

та

{\hat {a}}={\sqrt {\frac {m\omega }{2\hbar }}}\left(x+{\frac {ip}{m\omega }}\right)

Коли $\zeta$ дійсне, невизначеність $x$ та $p$ задається формулами

(\Delta x)^{2}={\frac {\hbar }{2m\omega }}\mathrm {e} ^{-2\zeta }

та

(\Delta p)^{2}={\frac {m\hbar \omega }{2}}\mathrm {e} ^{2\zeta }

Тому стиснені стани насичують принцип невизначеності Гайзенберга $\Delta x\Delta p={\frac {\hbar }{2}}$ , однак невизначеність однієї зі квадратурних змінних зменшена, а іншої — збільшена.

Виноски

Loudon, Rodney, The Quantum Theory of Light (Oxford University Press, 2000), [ISBN 0-19-850177-3]
D. F. Walls and G.J. Milburn, Quantum Optics, Springer Berlin 1994
C W Gardiner and Peter Zoller, "Quantum Noise", 3rd ed, Springer Berlin 2004
D. Walls, Squeezed states of light, Nature 306, 141 (1983)
R. E. Slusher et al., Observation of squeezed states generated by four wave mixing in an optical cavity, Phys. Rev. Lett. 55 (22), 2409 (1985)

.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Loudon, Rodney, The Quantum Theory of Light (Oxford University Press, 2000), [ISBN 0-19-850177-3]

[2] D. F. Walls and G.J. Milburn, Quantum Optics, Springer Berlin 1994

[3] C W Gardiner and Peter Zoller, "Quantum Noise", 3rd ed, Springer Berlin 2004

[4] D. Walls, Squeezed states of light, Nature 306, 141 (1983)

[slusher-5] R. E. Slusher et al., Observation of squeezed states generated by four wave mixing in an optical cavity, Phys. Rev. Lett. 55 (22), 2409 (1985)