Сітка з трикутників
Сітка з трикутників — це тип полігональної сітки, яка використовується у комп'ютерній графіці. Вона включає в себе набір трикутників (як правило, в тривимірному просторі), які мають спільні ребра або вершини.
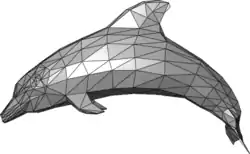
Багато графічних програмних пакетів і апаратних пристроїв можуть працювати більш ефективно з трикутниками, які згруповані в сітку, аніж коли опрацьовуються окремо. Це пов'язано з тим, що застосунки в комп'ютерній графіці виконують операції над спільними вершинами трикутників. У випадку окремих трикутників, система повинна опрацювати три вершини для кожного трикутника. Велика сітка може налічувати вісім або й більшу кількість трикутників, які мають спільну вершину — завдяки обробці однієї такої вершини лишень за один раз можна виконати частину роботи і досягти такого ж ефекту, як і при обробці вершин окремо. Багато застосунків комп'ютерної графіки використовують сітку з трикутників. Складовими сітки є вершини, ребра і трикутники. При виконанні застосунку може знадобитися знання різних з'єднань між компонентами сітки. Ці сполуки можуть оброблятись незалежно від фактичних координат вершин. Використовуються різні структури даних, вибір яких залежить від типу операцій над сіткою.
Представлення
Можливі різні методи зберігання та роботи з сіткою в комп'ютерній пам'яті. В OpenGL і DirectX API існує два основних способи проходження сітки з трикутників за допомогою графічного апаратного забезпечення: смуги з трикутників і індексація масивів.
Смуга з трикутників
Один із способів спільного використання даних про вершини між трикутниками є смуга трикутників. У смузі з трикутників кожен трикутник ділиться на одну повну грань з однією сусідньою і іншою із наступної. Іншим способом є віяло трикутників, яке представляє собою набір з'єднаних трикутників, які мають спільну центральну вершину. За допомогою цих методів вершини опрацьовуються ефективно, що призводить до необхідності обробляти лише N + 2 вершин, щоб намалювати N трикутників.
Смуги з трикутників є ефективними, проте недоліком є те, що не може бути тривіальним факт, яким чином зручно переводити довільну сітку з трикутників в смуги.
Структура даних
Структура даних, що представляє сітку, забезпечує підтримку двох основних операцій: вставки і видалення трикутників. Він також підтримує операцію руйнування грані, яка буде корисна в схемах проріджування трикутників. Структура не забезпечує підтримку позиції вершин, передбачається, що кожній вершині присвоюється унікальний цілочисельний ідентифікатор, як правило, індекс цієї вершини в масиві суміжних позицій вершин. Сітка з вершин визначається одним цілим числом і позначається як hvi. Сітка з граней визначається парою цілих чисел hv0,v1i, кожне є цілим числом, відповідним кінцевій точці ребра. Для формування відображення граней, грані зберігаються так, що v0 = min(v0,v1). Компонент трикутник визначається трійкою цілих чисел hv0,v1,v2i, кожне — ціле число, відповідне вершині трикутника. Для підтримки відображень трикутників, трикутники зберігаються так, що v0 = min(v0,v1,v2). Зауважимо, що hv0,v1,v2i та hv0,v2,v1i розглядаються як різні трикутники. В додаток двостороння трикутників, через що необхідно вставити обидві трійки в структуру даних. Заради уникнення постійних нагадувань щодо порядку індексів пари/трійки в іншій частині документа інформація не означає, що вершини впорядковані будь-яким чином (хоча реалізація обробляє порядок).
Зв'язок між компонентами повністю залежить від трійок, що представляють трикутники. Трикутник t = hv0,v1,v2i має вершини v0, v1, та v2. Йому належать грані e0 = hv0,v1i, e1 = hv1,v2i, та e2 = hv2,v0i. Відомі також зворотні зв'язки. Вершина v0 примикає до ребер е0 і е2 і до трикутнику t. Вершина v1 примикає до ребер e0 і e1 і до трикутнику t. Вершина v2 примикає до ребер e1 і e2 і до трикутнику t. Усі три грані e0, e1, e2 примикають до t.
Кількість інформації, що зберігається, в структурі даних залежить від потреб програми. Крім того, додаток може потребувати додаткової інформації, що зберігається в компонентах. Інформація, що зберігається в вершині, грані або трикутнику, називається атрибутом вершини, ребра або атрибут трикутника. Їх абстрактне представлення для простої структури даних, описані тут
Vertex = <integer>; // v Edge = <integer,integer>; // v0, v1 Triangle <integer,integer,integer>; // v0, v1, v2 VData = <application-specific vertex data>; EData = <application-specific edge data>; TData = <application-specific triangle data>; VAttribute = <VData,set<Edge>,set<Triangle>>; // data, eset, tset EAttribute = <EData,set<Triangle>>; // data, tset TAttribute = <TData>; // data VPair = pair<Vertex,VAttribute>; EPair = pair<Edge,EAttribute>; TPair = pair<Triangle,TAttribute>; VMap = map<VPair>; EMap = map<EPair>; TMap = map<TPair>; Mesh = <VMap,EMap,TMap>; // vmap, emap, tmap
Відображення підтримують стандартні функції вставки і видалення для хеш-таблиці. Вставка відбувається тільки якщо деталь вже не існує. Видалення відбувається тільки тоді, коли деталь існує.
Руйнування грані
Ця операція включає в себе визначення ребра hvk, vti, де vk називається зберігаючою вершиною, vt — направляючою. Трикутники, які містять ребро, видаляються з сітки. Вершина vt також видаляється з сітки. Спільна для будь-яких трикутників вершина vt буде замінена на vk.
Індексація масиву
За допомогою індексації масивів, сітка представлена двома окремими масивами: один масив містить вершини, а інший зберігає набори з трьох індексів в цьому масиві, які визначають трикутник. Графічна система обробляє вершини першого масиву і потім робить трикутники, використовуючи набори індексів, які працюють на перетворених даних.
Див. також
- Полігональна сітка
- Nonobtuse сітка
- Неоднорідний раціональний B-сплайн
- Хмара точок
- Moller-Trumbore алгоритм для променів трикутнику перетину
- Гіперграф