Топологічне сортування

Для графу ${\displaystyle G=({\bigl \{}2,3,5,7,8,9,10,11{\bigr \}},{\bigl \{}(3,8),(3,10),(5,11),(7,11),(7,8),(8,9),(11,2),(11,9),(11,10){\bigr \}}{\Bigr )}}$

Безконтурний орієнтований граф

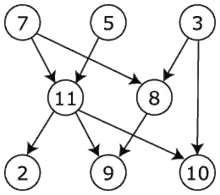
існує декілька узгоджених послідовностей його вершин, які можуть бути отримані за допомогою топологічного сортування, наприклад:

• ${\displaystyle 7,5,11,3,8,2,9,10}$
• ${\displaystyle 3,7,5,8,11,10,9,2}$
• ${\displaystyle 7,5,11,2,3,8,9,10}$

Видно, що в послідовності можуть брати участь будь-які дві вершини, що не входять у відношення часткового порядку ${\displaystyle E}$.

Час виконання для звичайного алгоритму топологічного сортування лінійний до кількості вершин плюс кількість ребер ${\displaystyle O(|V|+|E|).}$

Один з цих алгоритмів (Кан, 1962[1]) працює, вибираючи вершини в тому самому порядку, що і випадкове топологічне сортування. Спочатку знаходить набір «початкових вершин», які не мають ребер, що входять, і вставляє їх в набір S; щонайменше одна така вершина має існувати, якщо граф ациклічний. Тоді:

L ← Порожній список, що буде містити відсортовані елементи
S ← Набір вершин без ребер, що входять
доки S не порожнє виконати
    видалити вершину n з S
    вставити n в L
    для кожної вершини m з ребром e з n до m виконувати
        видалити ребро e з графу
        якщо m не має більше ребер, що входять тоді
            вставити m в S
якщо граф має ребра тоді
    вивести повідомлення про помилку (граф має принаймні один цикл)
інакше 
    вивести повідомлення (пропоноване топологічне сортування: L)

Якщо маємо справу з орієнтованим ациклічним графом, то алгоритм видасть рішення (не унікальне).

Альтернативний алгоритм базується на пошуку в глибину. Для цього алгоритму ребра вказуються у зворотному напрямку. Тобто якщо ребро іде з x до y, то це означає, що робота x залежить від роботи y (іншими словами робота y має бути завершена перед тим, як x зможе стартувати). Алгоритм проходить кожну вершину в графі в довільному порядку, започатковуючи пошук у глибину, що закінчується коли досягає вершину, яку вже відвідали з початку сортування:

L ← Порожній список, що буде містити відсортований набір вершин
S ← Набір всіх вершин

функція відвідати(вершина n)
    якщо n ще не була відвідана тоді
        помітити n як відвідану
        для кожної вершини m з ребром від n до m виконати
            відвідати(m)
        додати n до L

для кожної вершини n в S виконати
    відвідати(n)

За допомогою топологічного сортування будується коректна послідовність виконання дій, будь-яка з яких може залежати від іншої: послідовність проходження навчальних курсів студентами, збірки вихідних текстів програм за допомогою Makefile'ів.

• NIST Dictionary of Algorithms and Data Structures: topological sort
• Weisstein, Eric W. TopologicalSort(англ.) на сайті Wolfram MathWorld.