Трилінійні координати
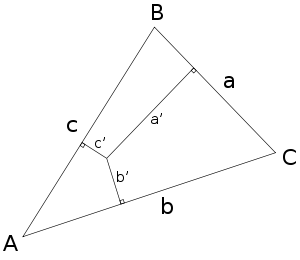
Трилінійні координати точки по відношенню до даного трикутника описуюють відносні відстані від трьох сторін цього трикутника. Трилінійні координати — це частковий випадок гомогенних координат.
Приклади
Інцентр має трилінійні координати 1 : 1 : 1; це означає що відстані від інцентру до сторін BC, CA, AB трикутника ABC пропорційні вказаним координатам, які визначаються абсолютними трилінійними координатами (r, r, r), де r — це радіус вписаного кола трикутника ABC. Відзначимо, що в записі x : y : z використовується двокрапка, що відрізняє трилінійні координати від відстаней. Через кому (kx, ky, kz) зазвичай записують абсолютні координати, які можна отримати з x : y : z використовуючи коефіцієнт:
де a, b, c — відповідні довжини сторін BC, CA, AB, а σ — площа трикутника ABC. (Розділення комою для трилінійних координат слід уникати тому що запис (x, y, z), який означає абсолютні координати, не дозволяє наприклад такого (x, y, z) = (2x, 2y, 2z), тоді як розділення двокрапкою це дозволяє x : y : z = 2x : 2y : 2z.)
Нехай A, B і C вершини довільного трикутника чи кути при відповідних вершинах. Тоді трилінійні координати для деяких відомих точок такі:
- A = 1 : 0 : 0
- B = 0 : 1 : 0
- C = 0 : 0 : 1
- інцентр = 1 : 1 : 1
- центроїд = bc : ca : ab = 1/a : 1/b : 1/c = csc A : csc B : csc C
- центр описаного кола = cos A : cos B : cos C
- ортоцентр = sec A : sec B : sec C
- центр кола дев'яти точок = cos(B − C): cos(C − A): cos(A − B)
Центри зовнівписаних кіл
- навпроти A = −1 : 1 : 1
- навпроти B = 1 : −1 : 1
- навпроти C = 1 : 1 : −1
Посилання
- Трилінійні координати на сайті MathWorld.(англ.)
- Кларк Кімберлінґ: Енциклопедія центрів трикутника. Список 3200 точок пов’язаних з трикутником.(англ.)