Вписане і зовнівписане в трикутник кола
Вписане в трикутник коло — коло всередині трикутника, що дотикається до всіх його сторін; найбільше коло, яке може перебувати всередині трикутника. Центр цього кола є точкою перетину бісектрис трикутника і називається інцентром трикутника.
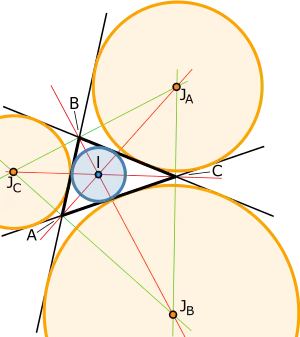
Зовнівписане коло трикутника — коло, що лежить поза трикутником і дотикається до одної сторони трикутника і продовження двох інших сторін. Будь-який трикутник має три різні позаписанних кола, кожна з яких стосується своєї сторони трикутника. Центром позаписанних кіл є перетин бісектриси одного внутрішнього кута і бісектрис двох інших зовнішніх кутів. Оскільки бісектриса внутрішнього кута перпендикулярна бісектрисі зовнішнього кута, центр вписаного кола разом з трьома центрами позаписанних кіл утворюють ортоцентричну систему[1].
Не всі багатокутники з числом сторін більше трьох мають вписане коло. Ті, які мають, називаються тангенціальними.
Примітки
- Roger A. Johnson. Advanced Euclidean Geometry. — Dover, 2007 (оригінал — 1929). — С. 189, #298(d).
Посилання
- Derivation of formula for radius of incircle of a triangle
- Weisstein, Eric W. Incircle(англ.) на сайті Wolfram MathWorld.
- Triangle incenter Triangle incircle Incircle of a regular polygon With interactive animations
- Constructing a triangle's incenter / incircle with compass and straightedge An interactive animated demonstration
- Equal Incircles Theorem at cut-the-knot
- Five Incircles Theorem at cut-the-knot
- Pairs of Incircles in a Quadrilateral at cut-the-knot
- An interactive Java applet for the incenter