Фазифікація
Фазифікація (англ. fuzzyfication) — перехід від чіткого значення деякого параметра до нечіткого значення деякої лінгвістичної змінної. Для здійснення такого переходу необхідна функція приналежності, що задає конкретну лінгвістичну змінну. Процес фазифікації передбачає попередній збір експертної інформації та використання процедур її обробки для побудови функцій приналежності вхідних величин.[1]
У контексті нечіткої логіки під фазифікацією розуміється не тільки окремий етап виконання нечіткого виведення, але і власне процес або процедура знаходження значень функцій приналежності нечітких множин (термів) на основі звичайних (чітких) вхідних даних. Фазифікацію ще називають введенням нечіткості.
Метою фазифікації є встановлення відповідності між конкретним (зазвичай чисельним) значенням окремої вхідної змінної системи нечіткого виведення і значенням функції приналежності відповідного їй терму вхідної лінгвістичної змінної.
Після завершення цього етапу для всіх вхідних змінних повинні бути визначені конкретні значення функцій приналежності по кожному з лінгвістичних термів, які використовуються в підумові бази продукційних правил системи нечіткого виведення.
Історія виникнення
Поняття «фазифікація» − одне з основних поняття нечіткої логіки, що було введено американським професором математики азербайджанського походження Лотфі Заде у 1965 р.
Процедура фазифікації
Формально процедура фазифікації виконується наступним чином. До початку цього етапу передбачаються відомими конкретні значення всіх вхідних змінних системи нечіткого виведення, тобто множина значень . У загальному випадку кожне , де − універсум лінгвістичної змінної .
Далі розглядається кожна з підумови виду правил системи нечіткого висновку, де − деякий терм з відомою функцією приналежності . При цьому значення використовується як аргумент , тим самим знаходиться кількісне значення . Це значення і є результатом фазифікації підумови.
Етап фазифікації вважається закінченим, коли будуть знайдені всі значення для кожної з підумови всіх правил, що входять у розглянуту базу правил системи нечіткого виводу. Цю множину значень позначимо через . При цьому якщо деякий терм лінгвістичної змінної не присутній ні в одному з нечітких висловлювань, то відповідне йому значення функції приналежності не знаходиться в процесі фазифікації.
Приклад фазифікації
Розглянемо приклад процесу фазифікації трьох нечітких висловлювань:
- «швидкість автомобіля мала»,
- «швидкість автомобілів середня»,
- «швидкість автомобіля висока»
для вхідної лінгвістичної змінної − «швидкість руху автомобіля».
Їм відповідають нечіткі висловлювання першого виду:
Припустимо, що поточна швидкість автомобіля дорівнює 55 км/год., тобто = 55 км/год.
Тоді фазифікація першого нечіткого висловлювання дає в результаті число 0, яке означає його ступінь істинності і виходить підстановкою значення км/год як аргументу функції приналежності терма (рис. 1).
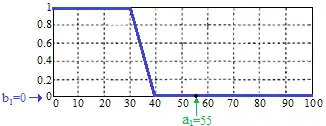
Фазифікація другого нечіткого висловлювання дає в результаті число 0.67 (наближене значення), яке означає його ступінь істинності і виходить підстановкою значення км/год як аргументу функції приналежності терма (рис. 2).
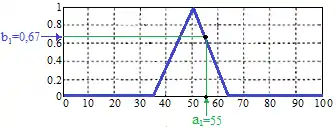
Фазифікації третього нечіткого висловлювання дає в результаті число 0, що означає його ступінь істинності і виходить підстановкою значення км/год як аргументу функції приналежності терма (рис. 3).
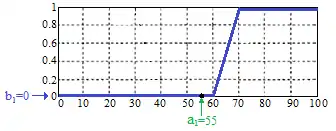
Місце фазифікації в системі нечіткого виведення
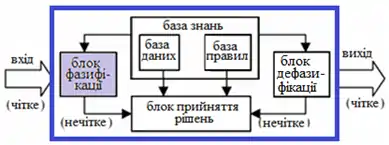
У системі нечіткого виведення (рис. 4) за етап фазифікації відповідає спеціальний блок — фазифікатор (блок фазифікації). Цей блок перетворює чіткі («crisp») величини, отримані за межами нечіткої системи, в нечіткі величини, що описуються лінгвістичними змінними в базі знань. Блок рішень використовує нечіткі продукційні правила, закладені в базі знань, для перетворення нечітких вхідних даних в необхідні виходи, які носять також нечіткий характер. Блок дефазифікації перетворює нечіткі дані з виходу блоку рішень в чітку величину для подальшого використання[2].
Див. також
Джерела інформації
- Леоненков, А. В. Нечеткое моделирование в среде MATLAB и fuzzyTECH / А. В. Леоненков. — СПб.: БХВ-Петербург, 2005. — 736 с.
- Штовба, С. Д. Введение в теорию нечетких множеств и нечеткую логику / С. Д. Штовба. — Винница: Издательство ВГТУ, 2001. — 198 с.
