Хвилі Лемба

Хвилі Лемба (англ. Lamb waves) — особливий тип хвиль, що поширюються в пружних хвилеводах. Хвилі названі ім'ям першого вченого Горація Лемба (англ. Horace Lamb), що знайшов дисперсійне співвідношення для цих хвиль і опублікував його в 1917 році. Такі хвилі є двовимірними збуреннями в нескінченному пружному шарі (область, що визначається відносно декартових координат нерівностями ${\displaystyle -h\leq z\leq h,-\infty \leq x\leq \infty ,-\infty \leq y\leq \infty }$). Для гармонічних хвиль з часовою залежністю для кінематичних і силових характеристик у вигляді ${\displaystyle e^{-i\omega t}}$ вирази для переміщень у напрямках координат ${\displaystyle x,z}$ мають вигляд:

${\displaystyle u_{x}=A_{x}f_{x}(\omega ,z)e^{i(\omega t-kx)}\quad \quad (1)}$

${\displaystyle u_{z}=A_{z}f_{z}(\omega ,z)e^{i(\omega t-kx)}\quad \quad (2)}$

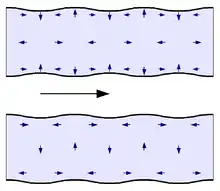
При вивченні властивостей хвиль Лемба розрізняють два типи хвильових рухів, що визначаються типами симетрії функції відносно товщинної координати ${\displaystyle z}$ у виразах (1) та (2). У випадку ${\displaystyle f_{x}(\omega z)=f_{x}(-\omega z)}$ говорять про симетричні хвилі Лемба. Характер руху частинок середовища в таких хвилях показано на верхній частині рисунка. Характер руху частинок в антисиметричному випадку ${\displaystyle f_{x}(\omega z)=-f_{x}(-\omega z)}$ показано на лижній частині рисунка. Уже в записі виразів для складових вектора переміщень (1) і (2) видно принципову різницю між хвилями в акустичних (заповнених рідиною чи газом) і в твердотільних пружних хвилеводах. У даному випадку функції товщинної координати ${\displaystyle z}$ залежать від частоти, що не спостерігається в акустичних хвилеводах[1].

Характер руху частинок пружного щару в симетричнх та антисиметричних хвилях Лемба. Стрілка вказує напрям осі ${\displaystyle ox}$.

Дослідження властивостей хвиль у хвилеводах починається з встановлення зв'язку між хвильовим числом ${\displaystyle k}$ та частотою ${\displaystyle \omega }$. Такі співвідношення визначають залежність фазової швидкості хвиль від частоти і називаються дисперсійними рівняннями Спочатку із рівнянь руху частинок пружного тіла знаходять вирази для функцій ${\displaystyle A_{x}f_{x}(\omega z)}$ та ${\displaystyle A_{z}f_{z}(\omega z)}$ а потім задовольняють умовам відсутності механічних напружень на поверхнях ${\displaystyle z=\pm h}$. Детально цей процес висвітлено в[2] В результаті одержано два дисперсійні рівняння, відповідно для симетричних та антисиметричних хвиль

${\displaystyle {\frac {\tan(\beta d/2)}{\tan(\alpha d/2)}}=-{\frac {4\alpha \beta k^{2}}{(k^{2}-\beta ^{2})^{2}}}\ \quad \quad \quad \quad (3)}$

${\displaystyle {\frac {\tan(\beta d/2)}{\tan(\alpha d/2)}}=-{\frac {(k^{2}-\beta ^{2})^{2}}{4\alpha \beta k^{2}}}\ \quad \quad \quad \quad (4)}$

тут

${\displaystyle \alpha ^{2}={\frac {\omega ^{2}}{c_{l}^{2}}}-k^{2}\quad \quad {\text{and}}\quad \quad \beta ^{2}={\frac {\omega ^{2}}{c_{t}^{2}}}-k^{2}.}$

У цих виразах для ${\displaystyle \alpha }$ та ${\displaystyle \beta }$ використано позначення ${\displaystyle c_{l}}$ та ${\displaystyle c_{t}}$, відповідно, для швидкості поздовжніх та поперечних хвиль в пружному тілі. Існування в пружному тілі двох типів хвиль суттєво ускладнює картину хвильових рухів у пружних хвилеводах. Фізичною причиною таких ускладнень є та обставина, що при відбитті при похилому падінні на вільну поверхню поздовжня хвиля віддає частину своєї енергії відбитій поперечній хвилі. Такий же процес спостерігається і при падінні на вільну границю поперечної хвилі, частину енергії якої забирає відбита поздовжня хвиля.

Попри досить простий вигляд дисперсійних рівнянь (3) і (4) кількісні оцінки характеристик хвиль Лемба та якісний аналіз залежності їхніх властивостей від частоти були проведені лише в 50-і роки XX століття в роботах Р. Д. Міндліна (R. D. Mindlin). Основні результати досліджень відтворено в першому томі серії книг, що присвячені проблемам фізичної акустики[3]. Було встановлено, що перші симетрична та антисиметрична хвилі Лемба поширюються при будь-якому значенні частоти. Зі зростанням частоти їхні фазові швидкості прямують до значення фазової швидкості хвилі Релея. Для інших хвиль більш високого порядку граничним значенням фазової швидкості є швидкість поперечних хвиль.