MAGENTA

MAGENTA — блочний шифр, розроблений Майклом Якобсоном і Клаусом Хубером для німецької телекомунікаційної компанії Deutsche Telekom AG. MAGENTA є скороченням від Multifunctional Algorithm for General-purpose Encryption and Network Telecommunication Applications (Багатофункціональний алгоритм для шифрування в загальних цілях і телекомунікаційних додатках).

Історія

Розробка MAGENTA почалася в 1990 році з основними принципами описаними в неопублікованій книзі[1]. Основна ідея полягала в застосуванні простої техніки, без магічних таблиць, яка могла бути виконана як апаратно, так і програмно. Плани полягали в розробці чипа, який міг би передавати дані зі швидкістю до 1 Гбіт/c і використовуватися для шифрування в ATM. На жаль, апаратна реалізація не отримала поширення, як планувалося, через вузьке застосування, але, незважаючи на це, дослідження показали, що такий чип можливо розробити[2]. MAGENTA брав участь в конкурсі AES в 1998 році, але вибув після першого раунду. Шифр став доступний учасникам конференції тільки в день презентації на відміну від інших шифрів, які брали участь у конурсі. MAGENTA використовувалася для шифрування даних всередині компанії Deutsche Telekom. Слід зазначити, що до MAGENTA швидке перетворення Фур'є в криптографічних цілях використовувалося в 2 шифрах. Конкретну назву першого не вдалося знайти[3]. Але відомо, що він винайдений Жан-П'єром Вассером і зареєстрований 2 червня 1959 року. Другим шифром є одна з реалізацій алгоритму A3 — Comp-128.

Шифрування

MAGENTA має структуру мережі Фейстеля. Раундова функція заснована на швидкому Адамаровому перетворенні[4], за винятком того, що замість додавання і віднімання на кожному етапі до одного з доданків застосовується S-блок, що задається функцією f(x), і потім вони складаються по модулю 2.

Нехай множина $B=\{0,1\}^{8}$ . Розмір блоку $M=(x_{0},...,x_{15})\in B^{16}$ вихідного тексту — 128 біт. Розмір ключа може приймати 3 значення:

128 біт : $K=(K_{1},K_{2})$ ,
192 біт : $K=(K_{1},K_{2},K_{3})$ ,
256 біт : $K=(K_{1},K_{2},K_{3},K_{4})$ , де $K_{1}=(y_{0},...,y_{7})\ K_{2}=(y_{8},...,y_{15})\ K_{3}=(y_{16},...,y_{23})\ K_{4}=(y_{24},...,y_{31})$ .

Нехай F — раундова функція. Шифр блоку M вираховується таким чином: $Enc_{K}(M)={\begin{cases}F_{K_{1}}(F_{K_{1}}(F_{K_{2}}(F_{K_{2}}(F_{K_{1}}(F_{K_{1}}(M)))))),&K=(K_{1},K_{2})\in B^{16},\\F_{K_{1}}(F_{K_{2}}(F_{K_{3}}(F_{K_{3}}(F_{K_{2}}(F_{K_{1}}(M)))))),&K=(K_{1},K_{2},K_{3})\in B^{24},\\F_{K_{1}}(F_{K_{2}}(F_{K_{3}}(F_{K_{4}}(F_{K_{4}}(F_{K_{3}}(F_{K_{2}}(F_{K_{1}}(M)))))))),&K=(K_{1},K_{2},K_{3},K_{4})\in B^{32};\end{cases}}$

128 біт — ключ К розбивається на 2 частини — К₁ та К₂. Кількість раундів 6. Ключі застосовуються в такому порядку:

Раунд	1	2	3	4	5	6
Застосований ключ	К₁	К₁	К₂	К₂	К₁	К₁

192 біт — ключ К розбивається на 3 частини — К₁, К₂ та К₃. Кількість раундів 6. Ключі застосовуютьсяу в таком порядку:

Раунд	1	2	3	4	5	6
Застосований ключ	К₁	К₂	К₃	К₃	К₂	К₁

256 біт — ключ К розбивається на 4 частини — К₁, К₂, К₃ та К₄. Кількість раундів 8. Ключі застосовуються в такому порядку:

Раунд	1	2	3	4	5	6	7	8
Застосованийй ключ	К₁	К₂	К₃	К₄	К₄	К₃	К₂	К₁

Дешифрування

Слід зауважити, що послідовність застосованих частин ключа, є паліндромом. Нехай $V(x_{0},...,x_{15})\ =\ (x_{8},x_{9},...,x_{15},x_{0},x_{1},...,x_{7})$ . Тоді

$V((Enc_{K}(x_{0},...,x_{15}))\ =\ Enc_{K}^{-1}(V(x_{0},...,x_{15})).$ [5][6]

Таким чином, дешифрування $Dec_{K}(M)\ =\ V(Enc_{K}(V(M))).$

Раундова функція F

Вхідний блок X розміром 128 біт раунду n з раундовим ключем K _n розбивається на 2 частини X₁ та X₂ розміром 64 біта кожна.

X = X₁X₂

Після проходження раунду отримуємо X^' = X₂F(X₂K_n)

З залежності ділення вихідного ключа від кількості раундів: довжина частини ключа, що використовується в кожному раунді завжди дорівнює 64 бітам.

Отже, функція F приймає 128-бітовий аргумент і повинна повертати 64-бітний (8-байтовий) результат.

Введемо допоміжні функції, через які потім виразимо F:

Функція	Розмір прийнятих аргументів	Розмір поверненого значения	Опис
f(x)	1 байт	1 байт	Повертає елемент з номером x в S-блоці
A(x, y)	1 байт	1 байт	f(x ⊕ f(y))
PE(x, y)	1 байт	2 байта	(A(x, y)A(y, x)) — конкатенує результати A(x, y) та A(y, x)
П(X)	16 байт	16 байт	X=X₀X₁...X₁₄X₁₅ (PE(X₀,X₈)PE(X₁,X₉)...PE(X₆,X₁₄)PE(X₇,X₁₅)) - конкатенує результати PE(X_i,X_i+8) i=0...7, X_i має розмір 1 байт.
T(X)	16 байт	16 байт	П(П(П(П(X)))) — застосовує до X 4 рази функцію П.
S(X)	16 байт	16 байт	(X₀X₂X₄…X₁₄X₁X₃X₅…X₁₅) — виконує перестановку байтів X: спочатку записуються байти з парним порядковим номером потім з непарним.
С(k, X)	k∈Ν X — 16 байт	16 байт	Рекурсивна функція: С(1,X) = T(X)) С(k, X) = T(X ⊕ S(C(k-1,X)))

Схема роботи функції П(X) :

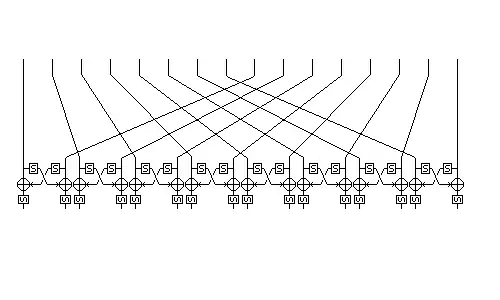
F вважають рівною першим 8 байтам від S(C(n, (X₂K_n))), тобто байтам C(n, (X₂K_n)) з парних порядковим номером. Спочатку n припустили рівним 7, але тести показали, що в цьому випадку шифр можливо зламати. Тому потім припустили n = 3. Як показали тести, це найкращий вибір, який не допускає криптографічних слабкостей, які позначаються на всьому шифрі. Таким чином,

F вважають рівною першим 8 байтам від S(C(3,(X₂K_n)))

S-блок

S-блок утворюється таким чином: Перший елемент — 1, наступні утворюються бітовим зсувом вліво попереднього, поки 1 не вийде за ліву межу байта. Відповідно початок блоку — 1 2 4 8 16 32 64 128

256₁₀=1 0000 0000₂, 1 вийшла за межі байта. В цьому випадку потрібно скласти по модулю 2 отримане зсунуте число 0000 0000₂ з числом 101₁₀=0110 0101₂:

0000 0000₂ ⊕ 0110 0101₂ = 0110 0101₂ = 101₁₀,тобто після 128 стоятиме 101.

101₁₀=0110 0101₂ << 1 = 1100 1010₂=202₁₀, 1 не вийшла за межу, відповідно наступний елемент 202.
202₁₀ << 1= 1100 1010₂ << 1 = 1001 0100₂, 1 вийла за межу:

1001 0100₂ ⊕ 0110 0101₂ = 1111 0001₂ = 241₁₀.

Останній 256 елемент вважається рівним 0. В результаті виходить такий S-блок:

   1    2    4    8   16   32   64  128
 101  202  241  135  107  214  201  247
 139  115  230  169   55  110  220  221
 223  219  211  195  227  163   35   70
 140  125  250  145   71  142  121  242
 129  103  206  249  151   75  150   73
 146   65  130   97  194  225  167   43
  86  172   61  122  244  141  127  254
 153   87  174   57  114  228  173   63
 126  252  157   95  190   25   50  100
 200  245  143  123  246  137  119  238
 185   23   46   92  184   21   42   84
 168   53  106  212  205  255  155   83
 166   41   82  164   45   90  180   13
  26   52  104  208  197  239  187   19
  38   76  152   85  170   49   98  196
 237  191   27   54  108  216  213  207
 251  147   67  134  105  210  193  231
 171   51  102  204  253  159   91  182
   9   18   36   72  144   69  138  113
 226  161   39   78  156   93  186   17
  34   68  136  117  234  177    7   14
  28   56  112  224  165   47   94  188
  29   58  116  232  181   15   30   60
 120  240  133  111  222  217  215  203
 243  131   99  198  233  183   11   22
  44   88  176    5   10   20   40   80
 160   37   74  148   77  154   81  162
  33   66  132  109  218  209  199  235
 179    3    6   12   24   48   96  192
 229  175   59  118  236  189   31   62
 124  248  149   79  158   89  178    0

Заглиблюючись в теорію, можна підсумувати: Нехай є Поле Галуа GF(2⁸) і багаточлен, який задає це поле — p(x)=x⁸+x⁶+x⁵+x²+1 і нехай α — примітивний елемент поля, p (α) = 0. Тоді елемент f (x) в S-блок за індексом x можна представити як $f(x)=\left\{{\begin{matrix}\alpha ^{x},&x\neq 255,\\0,&x=255;\\\end{matrix}}\right.$

Властивості використовуваних функцій

f(x)

Протягом одного виконання MAGENTA функція f (x) обчислюється 2304 рази для ключів в 128 і 192 біта і 3072 рази для ключа в 256 біт. Так як функція являє собою нелінійну частину алгоритму, вона має особливу важливість для аналізу всього алгоритму. Наступні властивості f(x) відомі:

F(x) — взаємно-однозначна функція, тобто перестановка над множиною B = {0,1} ⁸ — всіх восьмибітних двійкових векторів.
Дана перестановка може бути представлена як результат дії 6 незв'язаних циклів довжини 198 38 9 5 5 і 1. Згідно комбінаторному аналізу, ці значення — «нормальні» і не мають значних розбіжностей з подібними циклами для випадкових перестановок. Єдине число, що залишається на місці — 161.
∀x ∈ B в такого, що f(x) ∈ {1,2,…127} виконано: f(x+1) = 2∙f(x), де ∙ — добуток десяткових чисел.
∀(x, y)∈B² і таких, що f(x)∙f(y)∈{1,2,…255} виконано: f((x+y) mod 255) = f(x)∙f(y)
Якщо розглядати f(x) як вектор-функцію, тобто f(x) = (f₇(x), f₆(x),…f₀(x)), то кожна з 8 булевих функцій нелінійна та має степінь 7. Також всілякі нетривіальні XOR-комбінації цих функцій нелінійні.[7] Ще одна цікава властивість полягає в тому, що кожна така функція має 128 доданків.

Криптоаналіз

Диференціальний криптоаналіз

Виявляється, принаймні частина MAGENTA може бути розкрита методами даного криптоаналізу. В якості різниці між двома елементами (відкритими текстами або шифрами) береться складання по модулю 2 між цими елементами. Таке визначення різниці обумовлено частим використанням операції XOR в даному шифрі.

Рядкові індекси XOR-таблиці є всіма можливими різницями між відкритими текстами, а стовпцеві індекси — між шифротекстами. На перетині конкретної відмінності відкритих текстів, тобто рядкового індексу, і конкретної відмінності шифрів, тобто стовпчикового індексу, стоїть число пар відкритих текстів, які відповідають даним відмінностям, шифри яких розрізняються на стовпчиковий індекс. XOR-таблиця для функції f має розміри 256 * 256. Сума кожного рядка й стовпчика дорівнює 256. Перший елемент першого рядка (з індексом 0), що відповідає нульовій відмінності відкритих текстів і шифрів, дорівнює 256. Всі інші елементи першого рядка рівні 0. Аналогічно всі елементи 1 стовпчика, крім першого, рівного 256, рівні 0. Особливий інтерес для диференціального аналізу представляють великі значення — найбільше значення в цій таблиці дорівнює 8. Воно має місце при таких розбіжностях

Відмінності між відкритими текстами	Відмінності між шифрами
51	35, 66, 154, 155, 250
102	111, 114, 232, 233, 244
153	96, 97, 115, 229, 247
204	18, 19, 38, 207, 251

В інших осередках таблиці розташовані числа 0, 2, 4, 6. Максимальна ймовірність переходу для ненульових відмінностей — ${\tfrac {8}{256}}=2^{-5}$ .
Для функції PE — також були визначені максимальні значення — вони дорівнюють 36 для різниці у відкритому тексті (234, 234) і нульової різниці шифрів. Максимальна ймовірність переходу— ${\tfrac {36}{256^{2}}}$ ≈ ${\tfrac {1}{1820}}$ .
Максимальна ймовірність переходу для функції T — $2^{-20}$ , для C(3,X) — $2^{-60}$ . Так як число необхідних пар шифрів більше ніж величина, зворотна ймовірності переходу, даний тип диференціального аналізу, заснований на xor-таблицях, не застосовний до MAGENTA. Однак питання про інші типи залишається відкритим.

Лінійний криптоаналіз

Лінійна апроксимаційна таблиця для S-блоку була обчислена.[8]. Для функцій $f_{0},...,f_{7}$ і для кожної xor-суми $f_{0}\oplus f_{1},f_{0}\oplus f_{2},...,f_{0}\oplus f_{1}\oplus ...\oplus f_{7}$ , як і для всіх лінійних функцій, було визначено, як багато цифр значень в таблиці узгоджується з відповідними цифрами розглянутих лінійних функцій. У підсумку вийшло 255 значень між 0 і 256. Нормування полягало в відніманні 128. Всі значення в таблиці лежали на відрізку [-24; 26]. Дані значення відповідають очікуваним для довільно обраних $f_{0},...,f_{7}$ . Значення 26 виходить при наступних лінійних комбінаціях:

$f_{1}\oplus f_{2}\oplus f_{3},f_{1}\oplus f_{3}\oplus f_{4}\oplus f_{6},$

$f_{1}\oplus f_{3}\oplus f_{6},f_{2}\oplus f_{3}\oplus f_{4}\oplus f_{6},$

$f_{1}\oplus f_{4}\oplus f_{7},f_{2}\oplus f_{3}\oplus f_{5}\oplus f_{6},$

$f_{2}\oplus f_{6}\oplus f_{7},f_{3}\oplus f_{4}\oplus f_{5}\oplus f_{6}.$

Застосована англ. Piling-up lemma|лема про набігання знаків до раундової функції F( $p_{i}=0.6$ , l=12)

${\frac {1}{2}}+2^{l-1}\prod _{i=1}^{l}p_{i}\approx {\frac {1}{2}}+2\cdot 10^{-9}$ Отримане значення є верхньою межею найкращого афінного перетворення для F. Приблизно $p^{-2}$ пар відкритий текст — шифр потрібно, щоб використовувати афінне лінійне наближення з ймовірністю ${\frac {1}{2}}+p$ [8].З огляду на попередні результати, для атаки на F необхідно $2.5\cdot 10^{17}$ . Отже, завдяки нелінійності f (x), MAGENTA не вдасться зламати атаками, заснованими на лінійному криптоаналіз.

Примітки

K. Huber. Neue Kryptographische Verfahren durch Kombination von Operationen in endlichen K? Örpern mit der schnellen Walshtransformation. Unpublished manuscript, 1990.
K. Huber and S. Wolter. Telekom's MAGENTA algorithm for en- / decryption in the gigabit/sec range. In ICASSP 1996 Conference Proceedings, volume 6, pages 3233 — 3235, 1996..
J.P Vaseur. Verschl? Uesselungsanordnung mit Mischverdrahtung. Deutsches Patentamt Auslegeschrift 1148397, Anmeldetag: 2.Juni 1959 Auslegeschrift: 9.Mai 1963 Anmelder: Compagnie Generale de Telegraphie sans Fil, Paris.
S.Y. Kung. VLSI Array Processors. Prentice Hall, 1988.
M. Luby and C. Rackoff. How to construct pseudorandom permutations from pseudorandom functions. SIAM J. Computing, 17(2):373-386, April 1988.
J. Pieprzyk and B. Sadeghiyan. Design of Hashing Algorithms, volume 756 of Lecture Notes in Computer Science. Springer, 1993.
SIT GmbH. Abschlussbericht — Untersuchung eines universellen Kryptoalgorithmus. Technical report, SIT GmbH, 1994.
E. Biham. On Matsui's linear cryptanalysis. In Proc. EUROCRYPT '94, volume 658 of Lecture Notes in Computer Science, pages 81-91, 1995.

Посилання

M. J. Jacobson, Jr. and K. Hubery The MAGENTA Block Cipher Algorithm
J. J. G. Savard. The Computer Era. Towards the 128-bit era: AES Candidates. Magenta // A Cryptographic Compendium
El. Biham, Al. Biryukov, N. Ferguson, L. R. Knudsen, B. Schneier, Ad. Shamir Cryptanalysis of Magenta

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] K. Huber. Neue Kryptographische Verfahren durch Kombination von Operationen in endlichen K? Örpern mit der schnellen Walshtransformation. Unpublished manuscript, 1990.

[2] K. Huber and S. Wolter. Telekom's MAGENTA algorithm for en- / decryption in the gigabit/sec range. In ICASSP 1996 Conference Proceedings, volume 6, pages 3233 — 3235, 1996..

[3] J.P Vaseur. Verschl? Uesselungsanordnung mit Mischverdrahtung. Deutsches Patentamt Auslegeschrift 1148397, Anmeldetag: 2.Juni 1959 Auslegeschrift: 9.Mai 1963 Anmelder: Compagnie Generale de Telegraphie sans Fil, Paris.

[4] S.Y. Kung. VLSI Array Processors. Prentice Hall, 1988.

[5] M. Luby and C. Rackoff. How to construct pseudorandom permutations from pseudorandom functions. SIAM J. Computing, 17(2):373-386, April 1988.

[6] J. Pieprzyk and B. Sadeghiyan. Design of Hashing Algorithms, volume 756 of Lecture Notes in Computer Science. Springer, 1993.

[7] SIT GmbH. Abschlussbericht — Untersuchung eines universellen Kryptoalgorithmus. Technical report, SIT GmbH, 1994.

[линейный_криптоанализ-8] E. Biham. On Matsui's linear cryptanalysis. In Proc. EUROCRYPT '94, volume 658 of Lecture Notes in Computer Science, pages 81-91, 1995.